Một lớp học có 40 học sinh. Trong đó, có 1 lớp trưởng, 1 lớp phó, 1 bí thư chi đoàn và 1 thủ quỹ. Có 1 giáo viên cần gặp ngẫu nhiên 4 em học sinh. a) Tìm xác suất để giáo viên đó gặp được 1 lớp trưởng, 1 bí thư chi đoàn. b) Tìm xác suất để giáo viên đó gặp được 1 lớp trưởng, 1 lớp phó học tập hoặc gặp được một lớp trưởng, 1 thủ quỹ. c) Tìm xác suất để giáo viên đó gặp được 1 lớp trưởng, 1 bí thư chi đoàn, 1 lớp phó học tập và không gặp được thủ quỹ.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Không gian mẫu: \(C_{40}^4\)
a. Số cách thỏa mãn: \(1.1.C_{38}^2=C_{38}^2\)
Xác suất: \(P=\dfrac{C_{38}^2}{C_{40}^4}\)
b. Số cách thỏa mãn: \(1.2.C_{37}^2\)
Xác suất: \(\dfrac{2.C_{37}^2}{C_{40}^4}\)
c. Số cách: \(1.1.1.C_{36}^1=36\)
Xác suất: \(\dfrac{36}{C_{40}^4}\)
Câu c:
Chọn lớp trưởng: có 1 cách
Chọn bí thư đoàn: có 1 cách
Chọn lớp phó học tập: có 1 cách
Còn lại 37 học sinh, nhưng loại trừ đi thủ quỹ nên chỉ còn 36
Chọn 1 bạn còn lại trong 36 bạn này: \(C_{36}^1\) cách
Theo quy tắc nhân ta có số cách thỏa mãn: \(1.1.1.C_{36}^1\)

Đáp án A
Ta thấy trong các đối tượng ta cần chọn, thì chỉ có lớp phó phong trào không đòi hỏi điều kiện gì nên ta sẽ chọn ở bước sau cùng
Do đó chọn 1 ban cán sự ta cần thực hiện các bước sau
Bước 1: Chọn1 bạn nữ là lớp trưởng có 15 cách
Bước 2: Chọn 1 bạn nam làm lớp phó học tập có 18 cách
Bước 3: Chọn1 bạn nữ là thủ quỹ có 14 cách
Bước 4: Chọn 1 người trong số còn lại làm lớp phó phong trào có 30 cách
Vậy tất cả có 15 . 18 . 14 . 30 = 113400 cách cử 1 ban cán sự

Đáp án A
Ta thấy trong các đối tượng ta cần chọn, thì chỉ có lớp phó phong trào không đòi hỏi điều kiện gì nên ta sẽ chọn ở bước sau cùng
Do đó chọn 1 ban cán sự ta cần thực hiện các bước sau
Bước 1: Chọn1 bạn nữ là lớp trưởng có 15 cách
Bước 2: Chọn 1 bạn nam làm lớp phó học tập có 18 cách
Bước 3: Chọn1 bạn nữ là thủ quỹ có 14 cách
Bước 4: Chọn 1 người trong số còn lại làm lớp phó phong trào có 30 cách
Vậy tất cả có ![]() cách cử 1 ban cán sự
cách cử 1 ban cán sự

Chọn D
Lời giải. Ta có
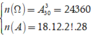
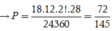
Chọn 1 nam trong 18 nam có 18 cách
Chọn 1 nữ trong 12 nam có 12 cách
Xếp chức danh bí thư, phó bí thư cho hai học sinh này có 2! cách
Còn 28 nên có 28 cách chọn ủy viên

Chọn 3 cán sự từ 40 học sinh: \(A_{40}^3\) cách
Chọn ban cán sự sao cho có 1 cặp song sinh (nhiều nhất cũng chỉ được 1 cặp thôi): chọn 1 cặp song sinh từ 4 cặp có 4 cách.
Chọn 1 người còn lại từ 38 người có 38 cách
Hoán vị 3 người có 3! cách
\(\Rightarrow4.38.3!\) cách chọn ban cán sự có 1 cặp song sinh
\(\Rightarrow A_{40}^3-4.38.3!\) cách chọn ban cán sự ko có cặp song sinh nào
Ví dụ các cặp song sinh là AB; CD; EF; GH
Giả sử bây giờ chọn cán sự gồm \(ACE\) chẳng hạn rõ ràng vẫn thỏa mãn, mặc dù nó rơi vào trường hợp em đã loại (người ta chỉ cấm 2 người đồng thời có mặt, 1 người thôi thì vẫn được, nhưng như cách chọn của em là cấm cả 2 rồi)

- Chọn lớp trưởng là học sinh nam có 22 cách.
- Chọn lớp phó văn nghệ là học sinh nữ có 18 cách.
- Chọn 2 bạn từ 38 học sinh còn lại và xếp vào 2 chỗ: phó bí thư và phó lao động, có: \(A^2_{38}\)
⇒ Có: \(22.18.A_{38}^2=556776\) (cách)

Chọn D
Gọi A là biến cố “4 học sinh được gọi có cả nam và nữ”, suy ra A ¯ là biến cố “4 học sinh được gọi toàn là nam hoặc toàn là nữ”
Số phần tử của không gian mẫu là ![]()
Ta có ![]()
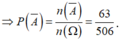
Vậy xác suất của biến cố A là
![]()

Đáp án : A
Để lựa chọn được hai ban thỏa mãn yêu cầu, ta chia làm hai công đoạn.
Công đoạn 1: Chọn một học sinh giỏi nữ, có 9 cách thực hiện.
Công đoạn 2. Chọn một học sinh giỏi nam, có 7 cách thực hiện.
Vậy theo quy tắc nhân, sẽ có 9.7=63 cách lựa chọn.
n(Ω) = \(C_{40}^4=91390\)
Kí hiệu A : "giáo viên gặp được lớp trưởng "
B : " giáo viên gặp được bí thư chi đoàn"
C : " giáo viên gặp được thủ quỹ "
D : " giáo viên gặp được lớp phó "
=> P(A) = P(B) = P(C) = P(D) = \(\dfrac{C_4^1}{C_{40}^4}\) ~ 0,00004
a) Cần tính \(P\left(A\cap B\right)\) = P(A) . P(B) = 0,000042
b) Cần tính \(P\left(\left(A\cap D\right)\cup\left(A\cap C\right)\right)\\ =P\left(A\cap D\right)+P\left(A\cap C\right)-P\left(A\cap D\right).P\left(A\cap C\right)\\ =P\left(A\right).P\left(D\right)+P\left(C\right).P\left(A\right)-P\left(A\right).P\left(D\right).P\left(A\right).P\left(C\right)\\ =2P^2\left(A\right)-P^4\left(A\right)\\ \)
c) cần tính \(P\left(A\right).P\left(B\right).P\left(D\right).\left(1-P\left(C\right)\right)\)