 Giải giúp em bài 8 9 10 đi ạ
Giải giúp em bài 8 9 10 đi ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




=> (x+x+...+x) + (1+2+...+10)=241
.....10x.....
=> 10x + [ (10+1).10 :2] = 240
=> 10x + 55 = 240
=> 10x = 240 - 55 = 185
=> x = 185 : 10 = 18,5

Số con thỏ sau khi bán còn lại số con là :
42-10=32(con thỏ )
Mỗi chuồng có số con thỏ là :
32:8=4(con thỏ )
Đáp số : 4 con thỏ

Đường thẳng y = ax + b đi qua A( -1; 2) và B( 2; -3)
Nên có hpt: \(\left\{{}\begin{matrix}-a+b=2\\2a+b=-3\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{5}{3}\\b=\dfrac{1}{3}\end{matrix}\right.\)
Vậy \(y=-\dfrac{5}{3}x+\dfrac{1}{3}\)
-> Chon B
Câu 9: ĐKXĐ: \(3-2x\ge0\)
\(\Leftrightarrow x\le\dfrac{3}{2}\)
-> Chọn B
Câu 10: Bấm máy là ra.

Bài 8:
a: Ta có: \(M=\dfrac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}+\dfrac{2\sqrt{x}+1}{\sqrt{x}-3}\)
\(=\dfrac{2\sqrt{x}-9-x+9+2x-4\sqrt{x}+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
b: Thay \(x=11-6\sqrt{2}\) vào M, ta được:
\(M=\dfrac{3-\sqrt{2}+1}{3-\sqrt{2}-3}=\dfrac{4-\sqrt{2}}{-\sqrt{2}}=-2\sqrt{2}+1\)
Bài 8:
a) \(M=\dfrac{2\sqrt{x}-9-\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)+\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{2\sqrt{x}-9-x+9+2x-3\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
b) \(M=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}=\dfrac{\sqrt{11-6\sqrt{2}}+1}{\sqrt{11-6\sqrt{2}}-3}=\dfrac{\sqrt{\left(3-\sqrt{2}\right)^2}+1}{\sqrt{\left(3-\sqrt{2}\right)^2}-3}=\dfrac{4-\sqrt{2}}{-\sqrt{2}}=1-2\sqrt{2}\)
c) \(M=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}=3\)
\(\Leftrightarrow3\sqrt{x}-9=\sqrt{x}+1\Leftrightarrow2\sqrt{x}=10\Leftrightarrow\sqrt{x}=5\Leftrightarrow x=25\left(tm\right)\)
d) \(M=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}< 1\)
\(\Leftrightarrow\sqrt{x}+1< \sqrt{x}-3\Leftrightarrow1< -3\left(VLý\right)\)
Vậy \(S=\varnothing\)
e) \(M=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}=1+\dfrac{4}{\sqrt{x}-3}\in Z\)
\(\Rightarrow\sqrt{x}-3\inƯ\left(4\right)=\left\{-4;-2;-1;1;2;4\right\}\)
Kết hợp đk:
\(\Rightarrow x\in\left\{1;16;25;49\right\}\)

ΔOMN vuông cân tại O và có OM = ON = a
⇒ MN = \(a\sqrt{2}\)
SOMN = \(\dfrac{OM.ON}{2}=\dfrac{a^2}{2}\)
Mặt khác \(S_{OMN}=\dfrac{OM+ON+MN}{2}.r_{OMN}\)
hay \(S_{OMN}=\dfrac{\left(2+\sqrt{2}\right)a}{2}.r_{OMN}\)
Vậy rOMN = \(\dfrac{2-\sqrt{2}}{2}a\)
c, do tam giác DKM đồng dạng tam giác DKC theo tỉ số đồng dạng là 1/2
=> Tỉ số diện tích là 1/4





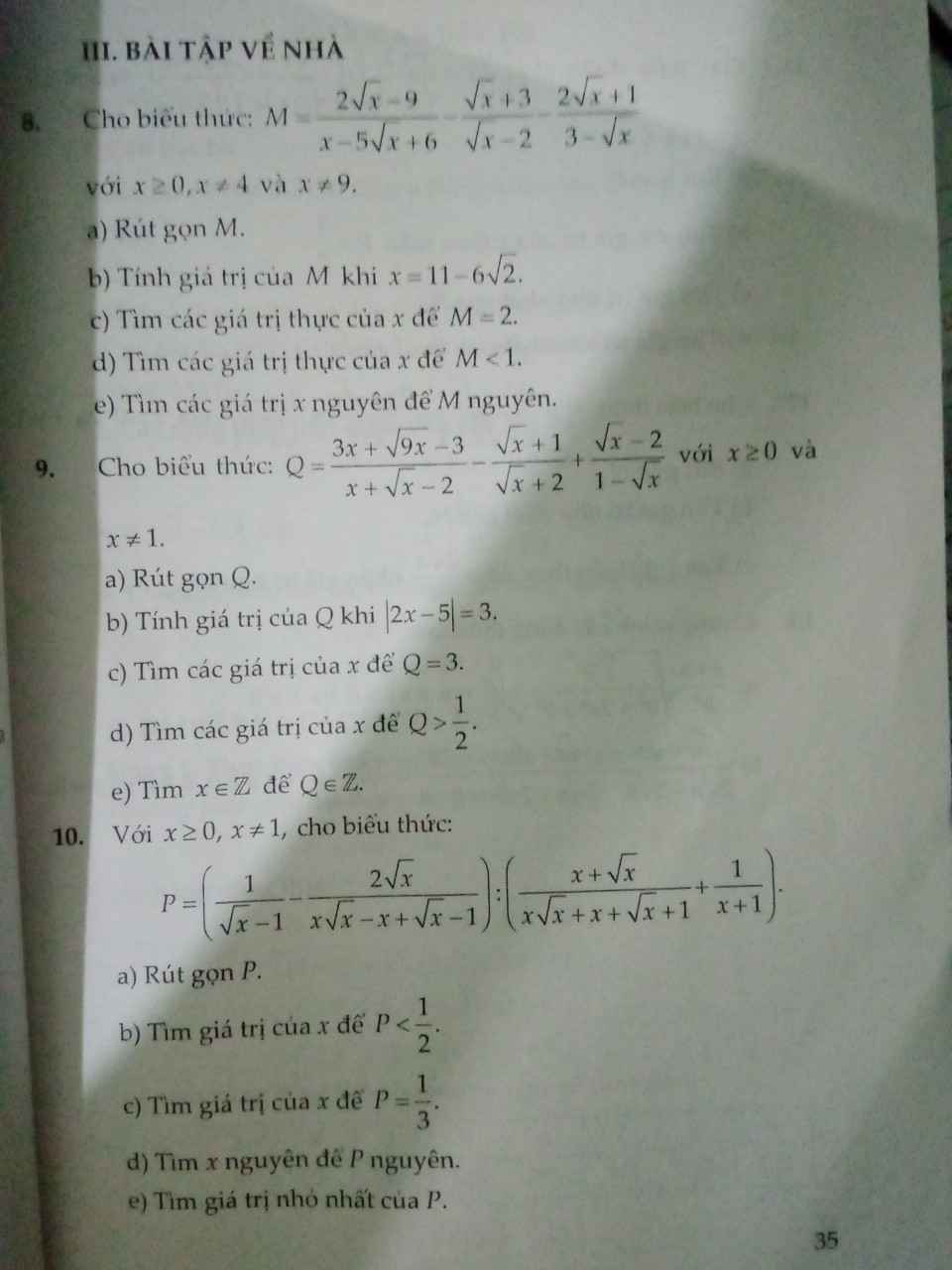

Bài 8.9.10 của câu 14 hay 15 bạn?
Câu 15:
1: Ta có: \(\dfrac{1}{1-\sqrt{2}}-\dfrac{1}{1+\sqrt{2}}\)
\(=\dfrac{1+\sqrt{2}-1+\sqrt{2}}{\left(1-\sqrt{2}\right)\left(1+\sqrt{2}\right)}\)
\(=-2\sqrt{2}\)
2: Ta có: \(\dfrac{1}{\sqrt{5}+1}+\dfrac{1}{\sqrt{5}-1}\)
\(=\dfrac{\sqrt{5}-1+\sqrt{5}+1}{\left(\sqrt{5}+1\right)\left(\sqrt{5}-1\right)}\)
\(=\dfrac{2\sqrt{5}}{4}=\dfrac{\sqrt{5}}{2}\)