Cho tam giác ABC có diện tích bằng 180cm2. Trên cạnh AB lấy hai điểm D và E sao cho AE = ED = DB. Trên cạnh AC lấy hai điểm M và N sao cho AM = MN = NC. Tính diện tích hình tứ giác DEMN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 8 2016
a) Diện tích tam giác ABC là: 48.100.1/2=2400(cm2) b) Diện tích tam giác BNC = 1/3 diện tích tam giác ABC. Vì: + Chung chiều cao hạ từ đỉnh B xuống AC + Đáy NC = 1/3 AC Diện tích tam giác BNC là: 2400:1/3=800(cm2) Diện tích tam giác BNA là: 2400-800=1600(cm2) c) Diện tích tam giác BNC = diện tích tam giác DNE = diện tích tam giác ENA. Vì: + Chung chiều cai hạ từ đỉnh N xuống đáy AB và đáy ED, AE, DB d) Diện tích tam giác ABN = 2/3 diện tích tam giác ABC. Vì: + Chung chiều cao hạ từ B xuống AC + Đáy AN = 2/3 AC Diện tích tam giác AEN = 1/3 diện tích ta giác ABN.Vì: + Chung chiều cao hạ từ N xuống AB + Đáy AE = 1/3 AB Diện tích tam giác ANE là: 1600.1/3=1600/3(cm2) Diện tích tam giác AEM=1/2 diện tích tam giác AEN.Vì: + Chung chiều cao hạ từ E xuống AN + Đáy AM = 1/2 AN Diện tích tam giác AEM là: 1600/3.1/2= 800/3(cm2) Diện tích hình thang DEMN là: 2400-800-800/3=4000/3(cm2) Đáp số:a) S ABC : 2400 cm2 b) S BNC : 800 cm2 S BNA:1600 cm2 c) S BND = S DNE = S ENA d) S DEMN : 4000/3cm2
N
8 tháng 8 2018
khuya rồi gửi đề dài ntn ai làm bn.....
...hỏi từng câu thôi
với lại đề copy đúng ko?(nhiều như vậy mà)
mai hỏi nha....mk ko muốn ngủ nhưng nhác trả lời^^
NT
13 tháng 2 2022
1. Cho tam giác ABC, D là điểm chính giữa cạnh BC, E là điểm chính giữa cạnh AC. Hai đoạn thẳng AD và BE cắt nhau tại I. Hãy so sánh diện tích tam giác AIE và BID.
CHỨNG MINH:
E là điểm giữa của AC
D là điểm giữa BC
=> ED là đường trung bình của tg ABC => ED // AB => khoảng cách từ E đến AB = khoảng cách từ D đến AB
Xét hai tg ABE và tg ABD có chung cạnh đáy AB; đường cao bằng nhau => SABE = SABD
Hai tgiác trên có phần diện tích chung là SAIB nên phần diện tích còn lại = nhau
=> SAIE = SBID
2. Cho tam giác ABC,đường cao AH = 48cm, BC = 100cm. Trên cạnh AB lấy các điểm E và D sao cho AE = ED = DB, trên cạnh AB lấy các điểm M và N sao cho AM = ED = DB, trên cạnh AC lấy các điểm M và N sao cho AM=MN=NC. Tính:
a) Diện tích tam giác ABC.
b) Diện tích tam giác BNC và tam giác BNA
c) Diện tích tam giác DEMN.
CHỨNG MINH:
a) Diện tích tg ABC là:
48 x 100 x 1/2 = 2400 (cm2)
b) Diện tích tg BNC = 1/3 diện tích tg ABC vì:
- Chung chiều cao hạ từ đỉnh B xuống AC
- Đáy NC = 1/3 AC
Diện tích tg BNC là:
2400 : 1/3 = 800 (cm2)
Diện tích tg BNA là:
2400 - 800 = 1600 (cm2)
c) Diện tích tg ABN = 2/3 ABC vì:
- Chung chiều cao hạ từ B xuống AC
- Đáy AN = 2/3 AC
Diện tích tg AEN = 1/3 ABN vì:
- Chung chiều cao hạ từ N xuống AB
- Đáy AE = 1/3 AB
Diện tích tg ANE là:
1600 x 1/3 = 1600/3 (cm2)
Diện tích tg AEM = 1/2 AEN vì:
- Chung chiều cao hạ từ E xuống AN
- Đáy AM = 1/2 AN
Diện tích tg AEM là:
1600/3 x 1/2 = 800/3 (cm2)
Diện tích hthang DEMN là:
2400 - 800 - 800/3 = 4000/3 (cm2)
:))
bài 3 chệu :((
26 tháng 5 2023
S ADM/S AEN=(AD/AE)^2=1/4
=>S DMNE/S AEN=3/4
=>S AEN=8cm2
=>S ABC=12cm2
7 tháng 4 2016
a) diện tích hai hình = nhau vì mỗi cạnh của hình tam giác ABC được phân chia = nhau cho nên hai hình tam giác đó = nhau
b) do ba hình ở đỉnh = nhau nên ta có : 360 : 3 = 120
vậy diện tích hình DEMNKH là : 360 - 120 = 240
đáp số : a) 120
:b)240
7 tháng 8 2023
Diện tích tam giác ABC = 60 x 30 : 2 = 900 (cm2)
Diện tích tam giác BKA = 2323 diện tích tam giác BAC
(vì cùng đường cao hạ từ B xuống AC và đáy KA = 2323AC)
Diện tích tam giác BKA là: 900×23= 600900×23= 600 (cm2)
Nối EK ta có:
Diện tích tam giác AEG = Diện tích tam giác EGK
(cùng đường cao hạ Từ E xuống AK. Đáy GA = GK)
Và diện tích tam giác KED = diện tích tam giác KDB
(Vì cùng đường cao hạ từ K xuống EB và đáy DE = DB)
Do đó:
Diện tích tam giác EGK + diện tích tam giác KED = diện tích tam giác EAG + diện tích tam giác KDB = 1212 diện tích tam giác BAK
Vậy diện tích tam giác EGK + diện tích tam giác KED = 600 : 2 = 300 (cm2)
Hay diện tích hình DEKG = 300 cm2
BD
22 tháng 6 2023
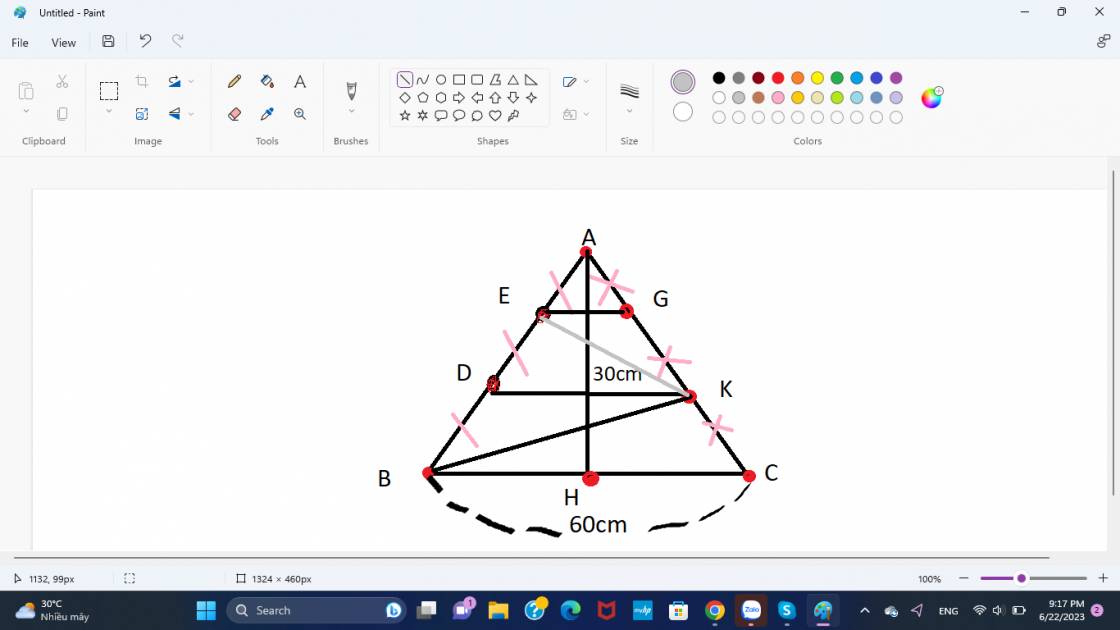
a) SABC : 60.30 :2 = 900(cm2)
b) Nối điểm E với điểm K
Ta có:
SEDK = SBDK ( vì chiều cao của 2 hình đều = \(\dfrac{1}{3}AH\) và đều hạ xuống đáy DK)
SEAG = SKDB ( vì chiều cao của 2 hình đều = \(\dfrac{1}{3}AH\) và đều hạ xuống đáy EG)
=> SEGK + SKED = SEAG + SKDB = \(\dfrac{1}{2}S_{BAK}\)
=> SDEGK = \(\dfrac{1}{2}S_{BAK}\)
\(\dfrac{S_{DEGK}}{S_{BAK}}=\dfrac{1}{2}\)