Cho hình vẽ:
Chứng minh Ax // Cy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 8 2021
a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến ứng với cạnh đáy BC
nên AM là đường cao ứng với cạnh BC
b: Xét tứ giác AMCI có
AI//MC
AM//CI
Do đó: AMCI là hình bình hành
mà \(\widehat{AMC}=90^0\)
nên AMCI là hình chữ nhật
hay AC=MI
c: Ta có: AICM là hình chữ nhật
nên AI=MC
mà MB=MC
nên AI=MB
Xét tứ giác AIMB có
AI//MB
AI=MB
Do đó: AIMB là hình bình hành
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
2 tháng 8 2023
Kéo dài AB cắt Cy tại E và kéo dài CB cắt Ax tại G như hình vẽ dưới đây:
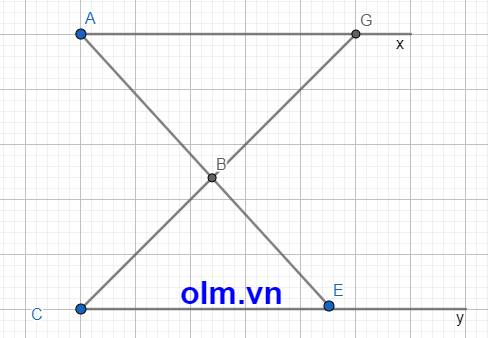
\(\widehat{ABC}\) = \(\widehat{GBE}\) (1) (vì đối đỉnh)
\(\widehat{GBE}\) = \(\widehat{BCE}\) + \(\widehat{CEB}\) (2) ( vì góc ngoài của tam giác bằng tổng hai góc trong không kề với nó)
\(\widehat{ABC}\) = \(\widehat{GAB}\) + \(\widehat{BCE}\) (3)
Từ (1); (2); (3) ta có: \(\widehat{BCE}\) + \(\widehat{CEB}\) = \(\widehat{GAB}\) + \(\widehat{BCE}\)
⇒ \(\widehat{CEB}\) = \(\widehat{GAB}\)
Mà hai góc CEB và góc GAB là hai góc ở vị trí so le trong nên
Cy // Ax (đpcm)
17 tháng 8 2021
a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến ứng với cạnh đáy BC
nên AM là đường cao ứng với cạnh BC
b: Xét tứ giác AMCI có
AM//CI
AI//MC
Do đó: AMCI là hình bình hành
mà \(\widehat{AMC}=90^0\)
nên AMCI là hình chữ nhật
Suy ra: AC=MI
c: Ta có: AMCI là hình chữ nhật
nên AI=MC
mà MC=MB
nên AI=MB
Xét tứ giác ABMI có
AI//MB
AI=MB
Do đó: ABMI là hình bình hành
PT
1
CM
14 tháng 5 2018
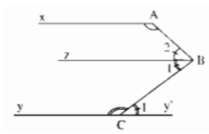
Kẻ Bz // Ax và Cy’ là tia đối của tia Cy
Ta có: ∠A +∠(B2 ) =180o
(2 góc trong cùng phía) (1)
Theo giả thiết ta có: ∠A +∠B + ∠C =360o (gt)
Hay ∠A +∠(B2 ) +∠(BCy) =360o (2)
Từ (1)và (2)suy ra :
∠(B1) + ∠BCy = 180o (3)
Lại có: ∠(C1 ) + ∠BCy =180o (hai góc kề bù) (4)
Từ (3) và (4) suy ra: ∠(B1 ) =∠(C1 )
Suy ra: Cy’ // Bz (vì có cặp góc so le trong bằng nhau)
Hay Cy // Bz mà Bz // Ax suy ra : Ax // Cy
PT
1
CM
20 tháng 2 2018
Kẻ tia Bz // Ax và Cy’ là tia đối của tia Cy.
Ta có: ∠(B2 ) +∠(xAB) =180o
(hai góc trong cùng phía)
Mà ∠(xAB) =140o(gt)
Suy ra: ∠(B2 ) =180-∠(xAB) =180o-140o=40o
Mà: ∠(B1 ) +∠(B2 ) =∠(ABC)
Suy ra ∠(B1 ) =∠(ABC) -(B2 ) =70o-40o=30o (1)
∠(yCB) +∠(BCy') =180o(2 góc kề bù)
∠BCy'=180o-∠(yCB) =180o-150o=30o (2)
Từ (1) và (2) ta có: ∠(B1 ) =∠(BCy')
Suy ra: Cy’ // Bz ( vì có cặp góc ở vị trí so le trong bằng nhau)
Hay Cy // Bz mà Bz // Ax suy ra Ax // Cy
H
0
NA
1
17 tháng 12 2023
Qua B kẻ tia Bz//Ax(Bz và Ax nằm khác phía so với đường thẳng AB)
Ta có: Bz//Ax
=>\(\widehat{zBA}=\widehat{xAB}\)
Ta có: \(\widehat{zBA}+\widehat{zBC}=\widehat{ABC}\)
\(\widehat{xAB}+\widehat{yCB}=\widehat{ABC}\)
mà \(\widehat{zBA}=\widehat{xAB}\)
nên \(\widehat{zBC}=\widehat{yCB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên Bz//Cy
mà Ax//Bz
nên Ax//Cy
KV
11 tháng 11 2023
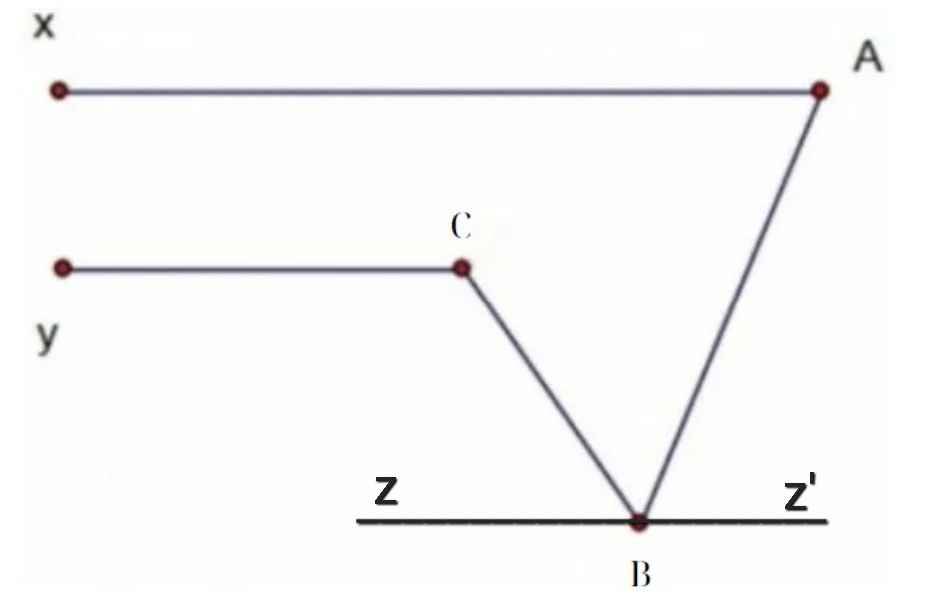Qua B vẽ đường thẳng zz' // Ax
⇒ ∠ABz' = ∠BAx = 50⁰ (so le trong)
⇒ ∠CBz' = ∠ABC + ∠ABz'
= 50⁰ + 80⁰
= 130⁰
⇒ ∠CBz' = ∠BCy = 130⁰
Mà ∠CBz' và ∠BCy là hai góc so le trong
⇒ zz' // Cy
Mà zz' // Ax
⇒ Ax // Cy
Kẻ tia Bz nằm trong góc ABC ,Bz//Cy
zBC+BCy=180 độ
zBC=180-150=30 độ
zBC+zBA=70 độ( Bz nằm giữa BA và BC)
zBA=70-30=40
zBA+BAx=180 độ
Mặt khác đó là 2 góc trong cùng phía
Bz//Ax
Bz//Cy
Ax//Cy
Kẻ Bz // Ax (1)
=> góc B1 = 40 độ (2 góc trong cùng phía)
Ta có : góc B1 + góc B2 = 70 độ
=> 40 độ + góc B2 = 70 độ
=> góc B2 = 30 độ
Lại có : góc B2 + góc C = 30 độ + 150 độ = 180 độ
Mà 2 góc này ở vị trí trong cùng phía
=> Bz // Cy (2)
Từ (1) và (2) => Ax // Cy (đpcm)