Cho tam giác ABC vuông tại A.Gọi d là đường thẳng vuông góc với BC tại C.Tia phân giác của góc B cắt AC ở D và cắt d ở E.Chứng minh rằng tam giác CDE có hai góc bằng nhau.
Mn giúp mk nha.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 12 2018
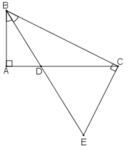
+) Ta có BD là tia phân giác của góc ABC nên: ∠(ABD) = ∠(DBC) (1)
+ Lại có: ∠(ADB)= ∠(CDE) ( hai góc đối đỉnh) (2)
+) Tam giác ABD vuông tại A nên:
∠ (ABD) + ∠(ADB) = 90° (tính chất tam giác vuông) (3)
Từ (1); (2) và (3) suy ra: ∠ (DBC) + ∠(CDE) = 90° (4)
+) Tam giác BCE vuông tại C nên:
∠ (DBC) + ∠(BEC) = 90° (tính chất tam giác vuông) (5)
Từ (4) và (5) suy ra : ∠ (CDE) = ∠(BEC)
Vậy tam giác CDE có hai góc bằng nhau.
G
15 tháng 11 2017
Tam giác vuông CBE có \(\widehat{E}+\widehat{B_1}=90^o\) (1)
Tam giác vuông ACD có \(\widehat{D_1}+\widehat{B_2}=90^o\) (2)
Mà \(\widehat{B_1}=\widehat{B_2}\) (tính chất phân giác) và \(\widehat{D_1}=\widehat{D_2}\)(đối đỉnh) nên suy ra \(\widehat{E}=\widehat{D_2}\)
=> Tam giác CDE cân ở C
NH
26 tháng 7 2019
(hình hơi xấu ạ :V)
\(\widehat{D_2}=\widehat{D_1}\), \(\widehat{D_1}\) phụ với \(\widehat{B_1}\) nên:
\(\widehat{D_2}\) phụ với \(\widehat{B_1}\) (1)
\(\widehat{E_1}\) phụ với \(\widehat{B_2}\) (2)
\(\widehat{B_1}=\widehat{B_2}\) (3)
Từ (1), (2), (3) => \(\widehat{D_2}=\widehat{E_1}\)
Có BE là tpg của ABC(gt)=>\(\widehat{ABE}=\widehat{CBE}\)(t/c tpg của góc)
Xét \(\Delta\)ABD vuông ở A có :
\(\widehat{ABD}+\widehat{BDA}\)=90o(hai góc phụ nhau trong \(\Delta\)vuông )
=>\(\widehat{ABE}+\widehat{BDA}\)=90o(D \(\in\)BE)(1)
Xét \(\Delta\)BCE vuông tại C có :
\(\widehat{CBE}+\widehat{BEC}\)=90o(hai góc phụ nhau trong \(\Delta\)vuông )(2)
Mà \(\widehat{ABE}=\widehat{CBE}\)(cmt)(3)
Từ (1),(2) và (3)
=>\(\widehat{BDA}=\widehat{BEC}\)
=>\(\widehat{BDA}=\widehat{DEC}\)(D\(\in\)BE)
mà \(\widehat{BDA}=\widehat{CDE}\)(đối đỉnh)
=>\(\widehat{DEC}=\widehat{CDE}\)
=> \(\Delta\)CDE là \(\Delta\)cân(t/c \(\Delta\)cân)
Vậy \(\Delta\)CDE là \(\Delta\)có 2 góc bằng nhau