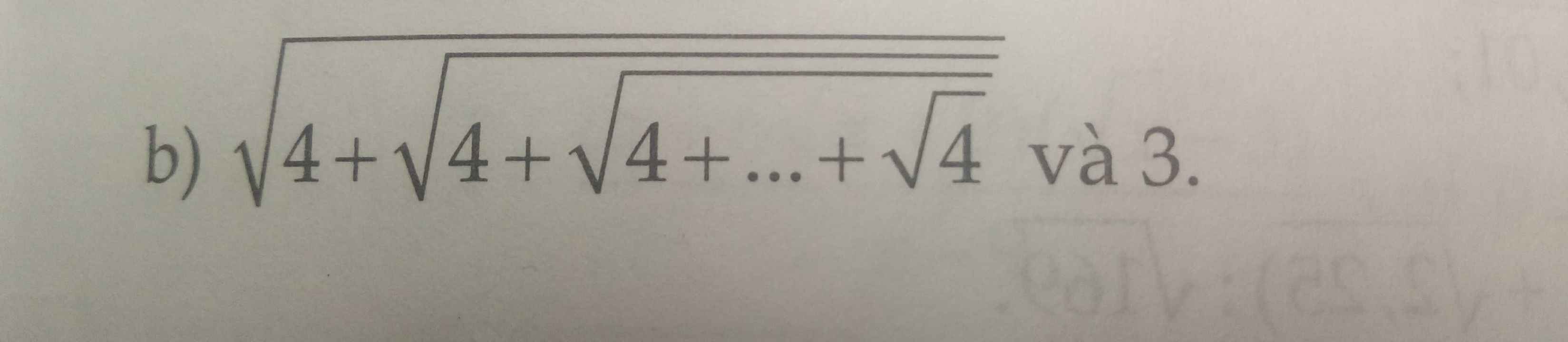So sánh \(\sqrt{4+\sqrt{4+\sqrt{4+\sqrt{4+...+\sqrt{4}}}}}\) với 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn xem lại đề nhé. Theo mình nghĩ thì không có căn 4 ở sau dấu.... Đây là vô hạn mà.


Bài này may mình có thi qua rùi.
Đặt
\(A=\sqrt{4+\sqrt{4+\sqrt{4+...+\sqrt{4}}}}>0\)
=> \(A^2=4+\sqrt{4+\sqrt{4+...+\sqrt{4}}}\)
=> A2 - A = 4
=> A2 - A - 4 = 0
Giải phương trình được 2 nghiệm:
\(A_1=\frac{1+\sqrt{17}}{2}\)
\(A_2=\frac{1-\sqrt{17}}{2}< 0\)( loại vì A>0)
Vậy \(A=\frac{1+\sqrt{17}}{2}< \frac{1+\sqrt{25}}{2}=\frac{1+5}{2}=3\)
Kết luận: \(\sqrt{4+\sqrt{4+\sqrt{4+...+\sqrt{4}}}}< 3\)
-------------
Chắc bạn ko hiểu chỗ A2 - A = 4 nhỉ?


Ta có:
\(R=\)\(\dfrac{3+\sqrt{5}}{2\sqrt{2}+\sqrt{3+\sqrt{5}}}+\dfrac{3-\sqrt{5}}{2\sqrt{2}-\sqrt{3-\sqrt{5}}}\)
\(=\)\(\dfrac{\sqrt{10}+3\sqrt{2}}{5+\sqrt{5}}+\dfrac{\sqrt{10}-3\sqrt{2}}{5-\sqrt{5}}\)
\(=\dfrac{4\sqrt{2}}{\sqrt{5}\left(\sqrt{5}+1\right)\left(\sqrt{5}-1\right)}\)
\(=\dfrac{4\sqrt{2}}{4\sqrt{5}}=\sqrt{\dfrac{2}{5}}\)
Làm câu S tương tự như này rồi đối chiếu kết quả nha

\(\left(\sqrt{4+\sqrt{5+\sqrt{6}}}\right)^2=4+\sqrt{5+\sqrt{6}};3^2=9=4+5\left(1\right)\\ \left(\sqrt{5+\sqrt{6}}\right)^2=5+\sqrt{6};5^2=25=5+20\left(2\right)\\ \left(\sqrt{6}\right)^2=6;20^2=400\\ \Leftrightarrow\sqrt{6}< 20\)
Thay vào \(\left(2\right)\Leftrightarrow\sqrt{5+\sqrt{6}}< 5\)
Thay vào \(\left(1\right)\Leftrightarrow\sqrt{4+\sqrt{5+\sqrt{6}}}< 3\)

\(\sqrt{4+\sqrt{4+\sqrt{4+\sqrt{4+...}}}}< \sqrt{6+\sqrt{6+\sqrt{6+...\sqrt{6+\sqrt{9}}}}}\)(100 dấu căn)
=> \(VT< \sqrt{6+\sqrt{6+\sqrt{6+...\sqrt{6+3}}}}=\sqrt{6+\sqrt{6+\sqrt{6+..\sqrt{6+\sqrt{9}}}}}\)(99 dấu căn)
=> \(VT< \sqrt{6+3}=3\)

Ta có:
\(\frac{1-\sqrt{n}+\sqrt{n+1}}{1+\sqrt{n}+\sqrt{n+1}}=\frac{\left(1-\sqrt{n}+\sqrt{n+1}\right)^2}{\left(1+\sqrt{n}+\sqrt{n+1}\right)\left(1-\sqrt{n}+\sqrt{n+1}\right)}=\frac{2n+2-2\sqrt{n}+2\sqrt{n+1}-2\sqrt{n\left(n+1\right)}}{2\left(1+\sqrt{n+1}\right)}\)
\(=\frac{\left[2n+2-2\sqrt{n}+2\sqrt{n+1}-2\sqrt{n\left(n+1\right)}\right]\left(1-\sqrt{n+1}\right)}{2\left(1+\sqrt{n+1}\right)\left(1-\sqrt{n+1}\right)}=\frac{-2n\sqrt{n+1}+2n\sqrt{n}}{-2n}=\sqrt{n+1}-\sqrt{n}\)
Suy ra:
\(Q=\sqrt{3}-\sqrt{2}+\sqrt{4}-\sqrt{3}+...+\sqrt{2017}-\sqrt{2016}=\sqrt{2017}-\sqrt{2}< \sqrt{2017}-1=R\)
Vậy Q < R.