Giúp mik câu f câu g câu k và câu m đi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



f: Thay x=0 và y=5 vào (d), ta được:
m-1=5
hay m=6
e: Thay x=1 và y=4 vào (d),ta được:
2m+3+m-1=4
=>3m+2=4
hay m=2/3

\(e,\left(x-2\right)^2-16=0\\ \Leftrightarrow\left(x-6\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=6\\x=-2\end{matrix}\right.\\ f,x^2-5x-14=0\\ \Leftrightarrow\left(x-7\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=7\\x=-2\end{matrix}\right.\\ g,8x\left(x-3\right)+x-3=0\\ \Leftrightarrow\left(8x+1\right)\left(x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{8}\\x=3\end{matrix}\right.\)

\(k,=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)+5\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{a}+\sqrt{b}+5}\\ =\dfrac{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}+5\right)}{\sqrt{a}+\sqrt{b}+5}=\sqrt{a}-\sqrt{b}\)
\(h,=\dfrac{1}{2a-1}\sqrt{25a^2\left(a^2-4a+4\right)}=\dfrac{1}{2a-1}\sqrt{25a^2\left(a-2\right)^2}\\ =\dfrac{\left|5a\left(a-2\right)\right|}{2a-1}=\left[{}\begin{matrix}\dfrac{5a\left(a-2\right)}{2a-1}\left(a\ge2;a\ne\dfrac{1}{2}\right)\\\dfrac{5a\left(2-a\right)}{2a-1}\left(0\le a< 2;a\ne\dfrac{1}{2}\right)\\\dfrac{-5a\left(2-a\right)}{2a-1}\left(a< 0\right)\end{matrix}\right.\)

Bài 2:
c: \(\left(\dfrac{3}{2}+x\right):1\dfrac{2}{5}=\dfrac{1}{2}\cdot\dfrac{3}{5}+0,2\)
=>\(\left(x+\dfrac{3}{2}\right):\dfrac{7}{5}=\dfrac{3}{10}+\dfrac{1}{5}=\dfrac{5}{10}=\dfrac{1}{2}\)
=>\(x+\dfrac{3}{2}=\dfrac{1}{2}\cdot\dfrac{7}{5}=\dfrac{7}{10}\)
=>\(x=\dfrac{7}{10}-\dfrac{3}{2}=\dfrac{7}{10}-\dfrac{15}{10}=-\dfrac{8}{10}=-\dfrac{4}{5}\)
f: \(-\dfrac{7}{5}-\left(\dfrac{2}{3}+x\right)=\dfrac{3}{10}\)
=>\(-\dfrac{7}{5}-\dfrac{2}{3}-x=\dfrac{3}{10}\)
=>\(x=-\dfrac{7}{5}-\dfrac{2}{3}-\dfrac{3}{10}=\dfrac{-42-20-9}{30}=\dfrac{-71}{30}\)
g: \(\left|x-\dfrac{1}{6}\right|-\dfrac{7}{12}=\dfrac{1}{4}\)
=>\(\left|x-\dfrac{1}{6}\right|=\dfrac{1}{4}+\dfrac{7}{12}=\dfrac{10}{12}=\dfrac{5}{6}\)
=>\(\left[{}\begin{matrix}x-\dfrac{1}{6}=\dfrac{5}{6}\\x-\dfrac{1}{6}=-\dfrac{5}{6}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{6}{6}=1\\x=-\dfrac{5}{6}+1=-\dfrac{4}{6}=-\dfrac{2}{3}\end{matrix}\right.\)
l: \(x:\left(\dfrac{1}{5}-\dfrac{7}{10}\right)=-2+\left(-1\dfrac{2}{3}\right)\)
=>\(x:\left(\dfrac{2}{10}-\dfrac{7}{10}\right)=-2+\dfrac{-5}{3}=\dfrac{-11}{3}\)
=>\(x:\dfrac{-1}{2}=-\dfrac{11}{3}\)
=>\(x=\dfrac{11}{3}\cdot\dfrac{1}{2}=\dfrac{11}{6}\)
k: \(x:\left(\dfrac{1}{7}-\dfrac{3}{14}\right)=-3+\left(-1\dfrac{2}{3}\right)\)
=>\(x:\left(\dfrac{2}{14}-\dfrac{3}{14}\right)=-3-\dfrac{5}{3}=\dfrac{-14}{3}\)
=>\(x:\dfrac{-1}{14}=\dfrac{-14}{3}\)
=>\(x=\dfrac{14}{3}\cdot\dfrac{1}{14}=\dfrac{1}{3}\)
Bài 3:
a: \(A=\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}\)
\(=\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+\dfrac{1}{4\cdot5}+\dfrac{1}{5\cdot6}+\dfrac{1}{6\cdot7}+\dfrac{1}{7\cdot8}\)
\(=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{7}-\dfrac{1}{8}\)
\(=\dfrac{1}{2}-\dfrac{1}{8}=\dfrac{3}{8}\)
b: \(B=\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}+\dfrac{1}{90}\)
\(=\dfrac{1}{4\cdot5}+\dfrac{1}{5\cdot6}+\dfrac{1}{6\cdot7}+\dfrac{1}{7\cdot8}+\dfrac{1}{8\cdot9}+\dfrac{1}{9\cdot10}\)
\(=\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{10}\)
\(=\dfrac{1}{4}-\dfrac{1}{10}=\dfrac{5-2}{20}=\dfrac{3}{20}\)

i) \(\sqrt{3+2\sqrt{2}}+\sqrt{\left(\sqrt{2}-2\right)^2}=\sqrt{\left(\sqrt{2}\right)^2+2.\sqrt{2}.1+1^2}+\left|\sqrt{2}-2\right|\)
\(=\sqrt{\left(\sqrt{2}+1\right)^2}+2-\sqrt{2}=\left|\sqrt{2}+1\right|+2-\sqrt{2}=\sqrt{2}+1+2-\sqrt{2}=3\)
k) \(\sqrt{4-\sqrt{15}}-\sqrt{4+\sqrt{15}}+\sqrt{6}=\sqrt{\dfrac{8-2\sqrt{15}}{2}}-\sqrt{\dfrac{8+2\sqrt{15}}{2}}+\sqrt{6}\)
\(=\sqrt{\dfrac{\left(\sqrt{5}\right)^2-2.\sqrt{5}.\sqrt{3}+\left(\sqrt{3}\right)^2}{2}}-\sqrt{\dfrac{\left(\sqrt{5}\right)^2+2.\sqrt{5}.\sqrt{3}+\left(\sqrt{3}\right)^2}{2}}+\sqrt{6}\)
\(=\sqrt{\dfrac{\left(\sqrt{5}-\sqrt{3}\right)^2}{2}}-\sqrt{\dfrac{\left(\sqrt{5}+\sqrt{3}\right)^2}{2}}+\sqrt{6}\)
\(=\dfrac{\left|\sqrt{5}-\sqrt{3}\right|}{\sqrt{2}}-\dfrac{\left|\sqrt{5}+\sqrt{3}\right|}{\sqrt{2}}+\sqrt{6}\)
\(=\dfrac{\sqrt{5}-\sqrt{3}}{\sqrt{2}}-\dfrac{\sqrt{5}+\sqrt{3}}{\sqrt{2}}+\sqrt{6}=\dfrac{-2\sqrt{3}}{\sqrt{2}}+\sqrt{6}=-\sqrt{6}+\sqrt{6}=0\)
m) \(2\sqrt{56}-14\sqrt{\dfrac{2}{7}}+\left(\sqrt{7}-\sqrt{2}\right)\sqrt{7}-\dfrac{8\sqrt{2}}{\sqrt{3}-\sqrt{7}}\)
\(=2\sqrt{4.14}-2\sqrt{49.\dfrac{2}{7}}+7-\sqrt{14}+\dfrac{8\sqrt{2}.\left(\sqrt{7}+\sqrt{3}\right)}{\left(\sqrt{7}-\sqrt{3}\right)\left(\sqrt{7}+\sqrt{3}\right)}\)
\(=4\sqrt{14}-2\sqrt{14}+7-\sqrt{14}+\dfrac{8.\left(\sqrt{14}+\sqrt{6}\right)}{4}\)
\(=\sqrt{14}+7+2\left(\sqrt{14}+\sqrt{6}\right)=7+3\sqrt{14}+2\sqrt{6}\)
Lời giải:
i.
\(=\sqrt{(\sqrt{2}+1)^2}+|\sqrt{2}-2|=|\sqrt{2}+1|+|\sqrt{2}-2|=\sqrt{2}+1+2-\sqrt{2}=3\)
k.
\(=\frac{1}{\sqrt{2}}(\sqrt{8-2\sqrt{15}}-\sqrt{8+2\sqrt{15}}+\sqrt{12})\)
\(=\frac{1}{\sqrt{2}}(\sqrt{(\sqrt{3}-\sqrt{5})^2}-\sqrt{(\sqrt{3}+\sqrt{5})^2}+2\sqrt{3})\)
\(=\frac{1}{\sqrt{2}}(|\sqrt{3}-\sqrt{5}|-|\sqrt{3}+\sqrt{5}|+2\sqrt{3})=\frac{1}{\sqrt{2}}(-2\sqrt{3}+2\sqrt{3})=0\)
m.
\(=4\sqrt{14}-2\sqrt{14}+7-\sqrt{14}-\frac{8\sqrt{2}(\sqrt{3}+\sqrt{7})}{(\sqrt{3}-\sqrt{7})(\sqrt{3}+\sqrt{7})}\)
\(=\sqrt{14}+7-\frac{8(\sqrt{14}+\sqrt{6})}{-4}=\sqrt{14}+\sqrt{7}+2(\sqrt{14}+\sqrt{6})=3\sqrt{14}+\sqrt{7}+2\sqrt{6}\)

 Giúp mình câu f,g,f,k với ạ
Giúp mình câu f,g,f,k với ạ
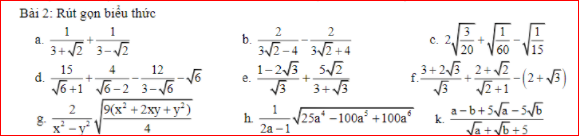
 giúp bài 3, câu c,f,g,l,k bài 2
giúp bài 3, câu c,f,g,l,k bài 2 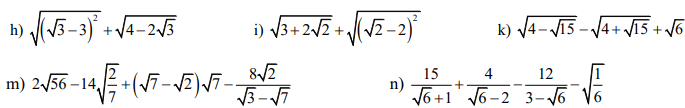

g) \(\dfrac{2}{5}-\dfrac{2}{5}x=\dfrac{2}{5}\)
\(\dfrac{2}{5}x=\dfrac{2}{5}-\dfrac{2}{5}\)
\(\dfrac{2}{5}x=0\)
⇒ \(x=0\)
f) \(\dfrac{2}{7}-\dfrac{8}{9}x=\dfrac{2}{3}\)
\(\dfrac{8}{9}x=\dfrac{2}{7}-\dfrac{2}{3}\)
\(\dfrac{8}{9}x=\dfrac{-8}{21}\)
\(x=\dfrac{-8}{21}-\dfrac{8}{9}\)
\(x=\dfrac{-80}{63}\)