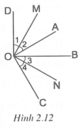
Trên cùng một nữa mặt phẳng bờ chứa tia Oa. Vẽ góc aob = 25 , góc aoc = 2.aob . Gọi oa' và oc' lần lượt là tia đối của oa và oc . Om là tia phân giác của góc a'oc . Chứng minh rằng :
a)Ob là tia phân giác của góc aoc .
b) Tia ob và tia om là hai tia đối nhau
Ai trả lời nhanh nhất thì được tick 5 lần