K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
1
29 tháng 12 2021
Câu 5:
\(\Leftrightarrow-x^2+7x-9+2x-9=0\)
\(\Leftrightarrow x^2-9x+18=0\)
=>x=3
=>Chọn A
DT
2
23 tháng 9 2021
40: Ta có: \(A=27x^3+8y^3-3x-2y\)
\(=\left(3x+2y\right)\left(9x^2-6xy+4y^2\right)-\left(3x+2y\right)\)
\(=\left(3x+2y\right)\left(9x^2-6xy+4y^2-1\right)\)
H9
HT.Phong (9A5)
CTVHS
21 tháng 9 2023
Các tập hợp tạo thành được:
\(\left\{a;b;c\right\};\left\{a;b;d\right\};\left\{a;b;đ\right\};\left\{a;b;e\right\};\left\{a;b;\text{ê}\right\};\\ \left\{a;c;d\right\};\left\{a;c;đ\right\};\left\{a;c;e\right\};\left\{a;c;\text{ê}\right\};\left\{a;d;đ\right\};\\ \left\{a;d;e\right\};\left\{a;d;\text{ê}\right\};\left\{a;đ;e\right\};\left\{a;\text{đ};\text{ê}\right\};\left\{a;e;\text{ê}\right\}\)
Có thể tạo thành 15 tập hợp
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
\(sin^2A+sin^2B+sin^2C=2\)
\(\Leftrightarrow sin^2A+\dfrac{1-cos2B}{2}+\dfrac{1-cos2C}{2}=2\)
\(\Leftrightarrow sin^2A-\dfrac{1}{2}\left(cos2B+cos2C\right)=1\)
\(\Leftrightarrow1-cos^2A-cos\left(B+C\right)cos\left(B-C\right)=1\)
\(\Leftrightarrow cos^2A+cos\left(B+C\right)cos\left(B-C\right)=0\)
\(\Leftrightarrow cos^2A-cosA.cos\left(B-C\right)=0\)
\(\Leftrightarrow cosA\left[cosA-cos\left(B-C\right)\right]=0\)
\(\Leftrightarrow cosA.sin\left(\dfrac{A+B-C}{2}\right)sin\left(\dfrac{A+C-B}{2}\right)=0\)
\(\Leftrightarrow cosA.sin\left(90^0-C\right)sin\left(90^0-B\right)=0\)
\(\Leftrightarrow cosA.cosB.cosC=0\)
\(\Leftrightarrow\left[{}\begin{matrix}A=90^0\\B=90^0\\C=90^0\end{matrix}\right.\) hay tam giác ABC vuông
LT
1
20 tháng 10 2023
a: ΔABC vuông tại B
=>\(\widehat{A}+\widehat{C}=90^0\)
=>\(\widehat{A}=50^0\)
Xét ΔBAC vuông tại B có
\(sinC=\dfrac{AB}{AC}\)
=>\(AC=\dfrac{6}{sin40}\simeq9,33\left(cm\right)\)
ΔBAC vuông tại B
=>\(BA^2+BC^2=AC^2\)
=>\(BC=\sqrt{9.33^2-6^2}\simeq7,14\left(cm\right)\)
b: ΔBAC vuông tại B có BH là đường cao
nên \(HC\cdot HA=BH^2\left(1\right)\)
ΔBHC vuông tại H có HI là đường cao
nên \(BI\cdot BC=BH^2\left(2\right)\)
Từ (1),(2) suy ra \(HC\cdot HA=BI\cdot BC\)
c: ΔBHA vuông tại H có HM là đường cao
nên \(BM\cdot BA=BH^2\left(3\right)\)
Từ (2),(3) suy ra \(BI\cdot BC=BM\cdot BA\)
=>\(\dfrac{BI}{BA}=\dfrac{BM}{BC}\)
Xét ΔBIM vuông tại B và ΔBAC vuông tại B có
\(\dfrac{BI}{BA}=\dfrac{BM}{BC}\)
Do đó: ΔBIM đồng dạng với ΔBAC
AM
0
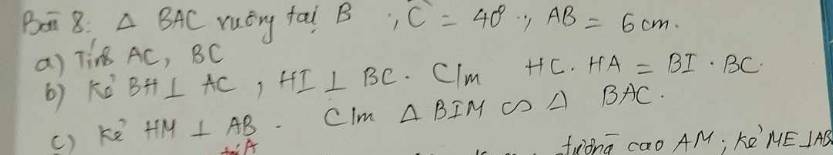
ô màu là điền số 18