Tìm một số tự nhiên có bốn chữ số. Biết rằng chữ số hàng nghìn, hàng trăm, hàng chục, hàng đơn vị tỉ lệ với 2; 1; 2; 3 và số đó chia hết cho 3
Các bạn giải chi tiết giúp mình đc k?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số cần tìm là abcd (a khác 0; 0 < b \(\le\) 9; 0 < c \(\le\)9; 0 < d \(\le\)9)
Theo đề bài ta có: \(\frac{a}{2}=\frac{b}{1}=\frac{c}{2}=\frac{d}{3}\)
Đặt \(\frac{a}{2}=\frac{b}{1}=\frac{c}{2}=\frac{d}{3}=k\Rightarrow a=2k,b=k,c=2k,d=3k\)
Do \(\hept{\begin{cases}a>0\\d\le9\end{cases}\Rightarrow0< k\le3}\) (1)
Vì \(\overline{abcd}⋮3\Rightarrow a+b+c+d=2k+k+2k+3k=8k⋮3\)
Mà \(8⋮̸3\Rightarrow k⋮3\) (2)
Từ (1) và (2) => k = 3
=> a = 6, b = 3, c = 6, d = 9
Vậy số cần tìm là 6369

4 số tự nhiên liên tiếp là n,n+1,n+2,n+3
viết theo hàng nghìn,trăm,chục ,đơn vị là
1000n+100(n+1)+10(n+2)+n+3=1111n+123
viết theo thứ tự ngược lại là
1000(n+3)+100(n+2)+10(n+1)+n=1111n+321...
vậy lớn hơn số ban đầu là 3210-123=3087
Gọi số hàng nghìn là a \(\Rightarrow\) 0<a<10
Số cần tìm là:
a.\(10^3\) +(a-1).\(10^2\) + (a+1).10 + (a+2)
a.(\(10^3\) + \(10^2\)+10+1) - 100 + 10 + 2
1111.a - 88 = 11.101.a - 8.11
11(101.a-8)
=> 101.a-8=11.\(n^2\)
( 101a - 8) chia hết 11
101 chia 11 dư 2 và -8 chia 11 dư 3
=> a=4
Với a = 4 => \(\dfrac{101.4-8}{11}=36=6^2\)
Vậy số cần tìm là: 4356

Vì chữ số hàng đơn vị gấp ba lần chữ số hàng chục nên chữ số hàng chục là: 9 : 3 = 3
Vì chữ số hàng trăm hơn chữ số hàng chục 4 đơn vị nên chữ số hàng trăm là: 3 + 4 = 7
Vì chữ số hàng nghìn kém chữ số hàng trăm hai đơn vị nên chữ số hàng nghìn là: 7 – 2 = 5
Vì chữ số hàng nghìn hơn chữ số hàng chục nghìn 1 đơn vị nên chữ số hàng chục nghìn là 5 – 1 = 4
Vì chữ số hàng chục nghìn gấp đôi chữ số hàng trăm nghìn nên chữ số hàng trăm nghìn là 4 : 2 = 2
Vậy số có 6 chữ số cần tìm là 245 739

Thamk khảo nhé
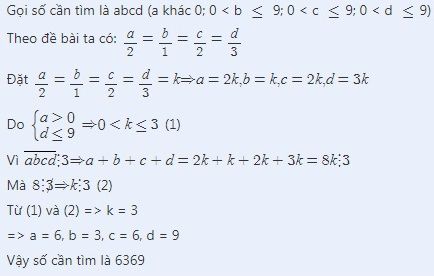
Sợ ko đúng T^T
CHúc các bn hok tốt
Em xin hết