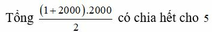từ 2000 số tự nhiên 1;2;3;...;2000, ta lấy ra k số bất kì sao cho trong các số vừa lấy luôn tìm được 2 số mà số này là bội của số kia. Tìm giá trị nhỏ nhất của k
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VV
7
HB
23 tháng 7 2015
a) Số số hạng từ 1 đến 2000 là :
( 2000 - 1 ) : 1 + 1 = 2000 ( số )
Tổng từ 1 đến 2000 là :
( 2000 + 1 ) x 2000 : 2 = 2001000
Vì 2001000 có tận cùng là 0 nên tổng chia hết cho 5
b) Số số hạng từ 1 đến 2001 là :
( 2001 - 1 ) : 1 + 1 = 2001 ( số )
Tổng từ 1 đến 2001 là :
( 2001 + 1 ) x 2001 : 2 = 2003001
Vì 2003001 có tận cùng là 1 nên không chia hết cho 2 mà 2003001 : 7 = 286143 nên tổng chia hết
chọn tôi đi
PT
1
PT
1
8 tháng 8 2015
1) Vì tích của 2000 số tự nhiên là số lẻ nên 2000 số đó là số lẻ
Tổng của 2 số lẻ là số chẵn => Tổng của 2000 số lẻ = tổng của 1000 số chẵn = số chẵn
Mà số 35 749 lẻ nên không có 2000 số tự nhiên thỏa mãn yêu cầu
2) Nếu đề của em là các số chia hết cho riêng từng số
- Số chia hết cho 5 là 5; 10; 15; ...; 2015
Từ số 5 đến 2015 có: (2015 - 5): 5 + 1 = 403 số
- Số chia hết cho 3 là 3; 6; ...; 2016
Từ số 3 đến 2015 có (2016 - 3) : 3 + 1 = 672 số
- Số chia hết cho 9 là 9; 18 ; ...; 2016
Từ 9 đến 2016 có (2016 - 9) : 9 + 1 = 224 số
- Số chia hết cho 10 là 10; 20; ...; 2010
=> có (2010 - 10): 10 + 1 = 201 số
PT
3
HD
1
L
2
28 tháng 9 2016
Số số hạng từ 1 đến 2000 là :
( 2000 - 1 ) : 1 + 1 = 2000 ( số )
Tổng dãy số liên tiếp từ 1 đến 2000 là :
( 2000 + 1 ) x 2000 : 2 = 2001000
Ví 2001000 có chữ số cuối cùng là 0 nên các số tự nhiên liên tiếp từ 1 đến 2000 chia hết cho 5
AY
28 tháng 9 2016
\(1+2+3+4+5+....+2000.\)
\(=\frac{1000-1+1}{2}.\left(2000+1\right)\)
\(=\frac{1000}{2}.2001\)
\(=500.2001\)
\(=1000500\)
Vì 1000500 tận cùng là 0 => tổng các số từ 1 đến 2000 chia hết cho 5.
21 tháng 10 2016
Khoảng cách giữa hai số liên tiếp:
2000-1999=1(đơn vị)
Số các số trong dãy trên:
(2000-1):1+1=2000(số)
Từ 1-> 9 có 9 số (số có 1 chữ số)
Từ 10->99 có 90 số (số có 2 chữ số)
Từ 100->999 có 900 số (số có 3 chữ số)
Từ 1000->2000 có 1001 số (số có 4 chữ số)
Số chữ số trong dãy trên:
1x9+2x90+3x900+4x1001=6893 (chữ số)
Đáp số: 6893 chữ số