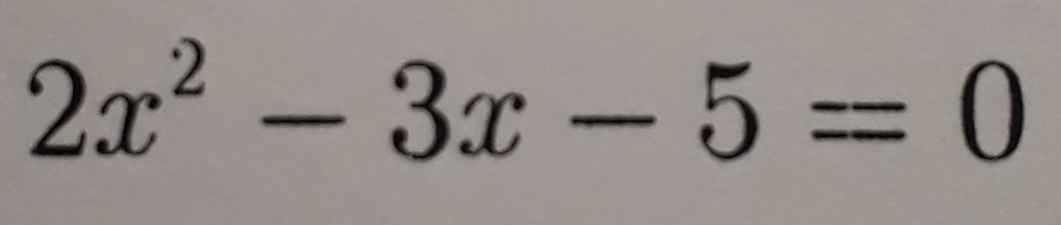Hãy cho mình các bài tập về giải phương trình bằng sơ đồ hoocne ( phương trình bậc cao )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Mô tả thuật toán phương trình bậc nhất ax + b = 0 như sau:
1. Nhập giá trị của a và b từ bàn phím.
2. Nếu a=0:
- Nếu b=0, phương trình vô số nghiệm
- Nếu b=0, phương trình vô nghiệm.
3. Nếu a khác 0, x = -b/a.
4. Hiển thị giá trị của x trên màn hình.

a) Quan sát vào độ thị ta thấy đoạn mà đồ thị nằm dưới truch hoành là \(\left[ { - 2;\frac{5}{2}} \right]\)
Vậy nghiệm của bất phương trình \({x^2} - 0,5x - 5 \le 0\) là đoạn \(\left[ { - 2;\frac{5}{2}} \right]\)
b) Quan sát vào đồ thị ta thấy đồ thị luôn nằm dưới trục hoành
Vậy nghiệm của bất phương trình \( - 2{x^2} + x - 1 > 0\) vô nghiệm

\(2x^2-3x-5=0 \\ \Leftrightarrow2x^2+2x-5x-5=0\\ \Leftrightarrow2x\left(x+1\right)-5\left(x+1\right)=0\\ \Leftrightarrow\left(2x-5\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2x-5=0\\x+1=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}2x=5\\x=-1\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-1\end{matrix}\right.\\ Vậy.S=\left\{\dfrac{5}{2};-1\right\}\)
\(2x^2-3x-5=0\)
\(\Leftrightarrow2x^2+2x-5x-5=0\)
\(\Leftrightarrow2x\left(x+1\right)-5\left(x+1\right)=0\)
\(\Leftrightarrow\left(2x-5\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-5=0\\x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-1\end{matrix}\right.\)
Vậy \(x=\dfrac{5}{2};x=-1\) là các nghiệm của phương trình.
#\(Toru\)

Tham khảo nhé bạn:
a. Những chất điều chế bằng pứ hóa hợp: H2O;SO2;CuO;CO2;CaO;MgOH2O;SO2;CuO;CO2;CaO;MgO
2H2+O2to→2H2O2H2+O2→to2H2O
S+O2to→SO2↑S+O2→toSO2↑
2Cu+O2to→2CuO2Cu+O2→to2CuO
C+O2to→CO2↑C+O2→toCO2↑
2Ca+O2to→2CaO2Ca+O2→to2CaO
Mg+O2to→MgOMg+O2→toMgO
b.
b. Những chất điều chế bằng pứ phân hủy: SO2:CuO;CO2;CaO;MgOSO2:CuO;CO2;CaO;MgO
BaSO3to→BaO+SO2↑BaSO3→toBaO+SO2↑
Cu(OH)2to→CuO+H2OCu(OH)2→toCuO+H2O
FeCO3to→FeO+CO2↑FeCO3→toFeO+CO2↑
CaCO3to→CaOO+CO2↑CaCO3→toCaOO+CO2↑
MgCO3to→MgO+CO2↑MgCO3→toMgO+CO2↑
- Phản ứng hóa hợp là phản ứng gồm 2 hay nhiều chất tham gia và chỉ tạo thành 1 chất sản phẩm
- Phản ứng phân hủy là phản ứng gồm 1 chất tham gia và chỉ tạo thành 2 hay nhiều chất sản phẩm , phản ứng cần nhiệt độ
Bài 2:
a, SO2
b, CO
c,
- Mn2O7
d, d, PbO2
Bài 3:
Giải thích các bước giải:
Gọi kim loại hóa trị II là R.⇒Oxit: ROPTHH: RO+H2O→R(OH)2mR(OH)2=200×8,55%=17,1 g.Áp dụng ĐLBT khối lượng ta có:mH2O=mbazơ−moxit=17,1−15,3=1,8 g.⇒nH2O=1,818=0,1 mol.Theo pt: nRO=n−H2O=0,1 mol.⇒MRO=15,30,1=153 g/mol.⇒MR+16=153⇒MR=137 (Ba)⇒Oxit: BaO

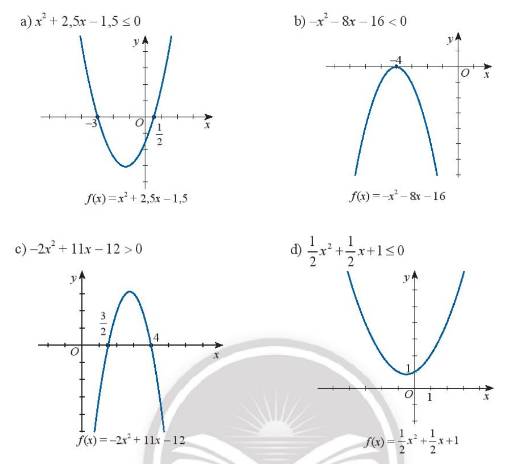
a) Dựa vào đồ thị ta thấy \({x^2} + 2,5x - 1,5 \le 0\) khi x thuộc đoạn \(\left[ { - 3;\frac{1}{2}} \right]\)
Vậy nghiệm của bất phương trình \({x^2} + 2,5x - 1,5 \le 0\) là \(\left[ { - 3;\frac{1}{2}} \right]\)
b) Dựa vào đồ thị ta thấy \( - {x^2} - 8x - 16 < 0\) với mọi x khác \( - 4\)
Vậy nghiệm của bất phương trình \( - {x^2} - 8x - 16 < 0\) là \(\mathbb{R}\backslash \left\{ { - 4} \right\}\)
c) Dựa vào đồ thị ta thấy \( - 2{x^2} + 11x - 12 > 0\) khi x thuộc khoảng \(\left( {\frac{3}{2};4} \right)\)
Vậy nghiệm của bất phương trình \( - 2{x^2} + 11x - 12 > 0\) là \(\left( {\frac{3}{2};4} \right)\)
d) Dựa vào đồ thị ta thấy đồ thị của tam thức \(f\left( x \right) = \frac{1}{2}{x^2} + \frac{1}{2}x + 1\) nằm hoàn toàn phía trên trục hoành với mọi x
Vậy bất phương trình \(\frac{1}{2}{x^2} + \frac{1}{2}x + 1 \le 0\) vô nghiệm.

Gọi x1,x2 là các nghiệm của phương trình đã cho
Áp dụng hệ thức Vi-et,ta có :
x1 + x2 = -5 ; x1x2 = -1
gọi y1,y2 là các nghiệm của phương trình phải lập,ta được :
y1 + y2 = x14 + x24 , y1y2 = x14x24
Ta có : x12 + x22 = ( x1 + x2 )2 - 2x1x2 = 25 + 2 - 27
Do đó : y1 + y2 = x14 + x24 = ( x12 + x22 )2 - 2x12x22 = 729 - 2 = 727
y1y2 = ( x1x2 )4 = 1
Từ đó pt phải lập có dạng : y2 - 727y + 1 = 0
Ta co: P = -1 <0
=> (1) có 2 nghiệm phân biệt khác dấu
Gọi hai nghiệm đó là \(x_1;x_2\)
=> \(x_1+x_2=-5;x_1.x_2=-1\)
Ta có: \(\left(x_1.x_2\right)^4=\left(-1\right)^4=1\)
\(\left(x_1\right)^4+\left(x_2\right)^4=\left(x_1^2+x_2^2\right)^2-2x_1^2x_2^2=\left[\left(x_1+x_2\right)^2-2x_1x_2\right]^2-2x_1^2x_2^2\)
\(=\left[\left(-5\right)^2-2.\left(-1\right)\right]^2-2.\left(-1\right)^2\)
\(=727\)
=> Phương trình có các nghiệm lũy thừa bậc 4 của các nghiệm phương trình (1) là:
\(x^2-727x+1=0\)

Ta có: I(-1,5; 4,5), J(1; 2)
*x = -1,5 là nghiệm của phương trình 2 x 2 + x – 3 = 0 vì:
2 - 1 , 5 2 + (-1,5) – 3 = 4,5 – 4,5 = 0
*x = 1 là nghiệm của phương trình 2 x 2 + x – 3 = 0 vì:
2. 1 2 + 1 – 3 = 3 – 3 = 0