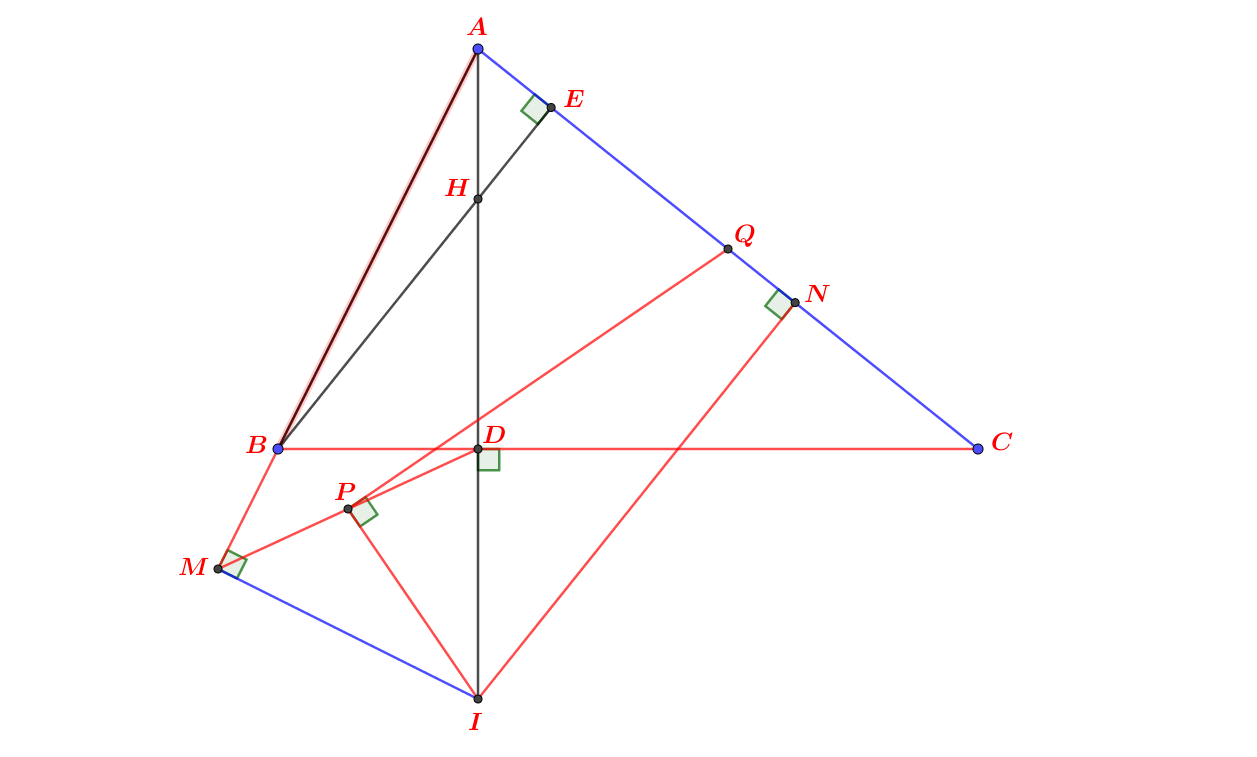
Cho tam giác ABC nhọn, \(\widehat{ABC}=60^o\)với hai đường cao AD, BE cắt nhau tại H. Tia CH cắt AB tại F. Gọi M là trung điểm của AC.
a,HF.HC=AH.DH
DB.DC=DH.AD
b, \(\widehat{AFE}=\widehat{ACB}\); EB là tia phân giác của \(\widehat{DEF}\)
Giải giúp mình với