1/ Cho hình nón có bán kính đáy bằng 3m, diện tích toàn phần bằng 24\(\pi\)m2 . Tinh thể tích hình nón
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 10 2018
Chọn D.
Phương pháp:
Cách giải:
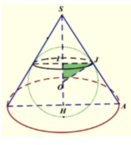
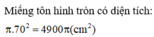
Gọi bán kính đáy và chiều cao của hình nón lần lượt là r , h ( r , h > 0 ) .
CM
1 tháng 2 2018
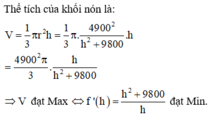
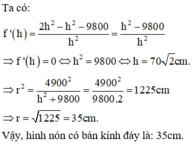
Đáp án D
Gọi l là độ dài đường sinh của hình nón.
Vì bán kính hình cầu và bán kính đáy của hình nón bằng nhau nên từ giả thiết ta có:
CM
9 tháng 10 2018
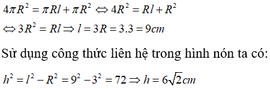
Đáp án D
Gọi l là độ dài đường sinh của hình nón.
Vì bán kính hình cầu và bán kính đáy của hình nón bằng nhau nên từ giả thiết ta có:
15 tháng 6 2021
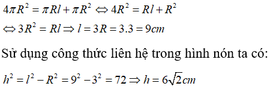
\(1.Sxq=\pi Rl=\pi3.5=15\pi cm^2\)
\(Stp=Sxq+\pi R ^2=15\pi+9\pi=24\pi cm^2\)
\(2.V=\dfrac{1}{3}\pi R^2.\sqrt{l^2-R^2}=\dfrac{1}{3}\pi.3^2.\sqrt{5^2-3^2}=12\pi cm^3\)
CM
7 tháng 12 2019
Chọn C.
Phương pháp:
Công thức liên hệ giữa bán kính đáy, chiều cao và đường sinh của hình nón:
Diện tích xung quanh của hình nón :
Diện tích toàn phần của hình nón :
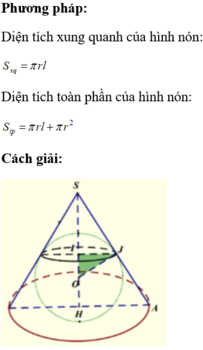
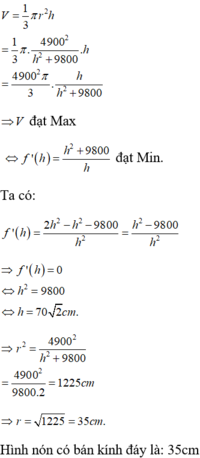
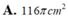
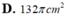
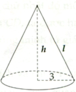
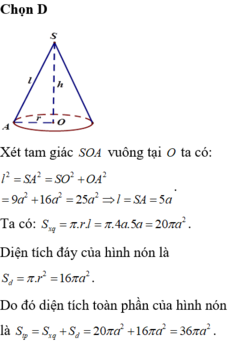
\(S_{\text{mặt đáy}}:\pi.3^2=9\pi\left(cm^2\right)\)
\(S_{\text{xung quanh}}:\pi rl=\pi.3.l=24\pi-9\pi=15\pi\Rightarrow l=5\left(cm^2\right)\)
\(\text{Chiều cao khối chóp}:h=\sqrt{l^2-r^2}=\sqrt{5^2-3^2}=4\left(cm\right)\)
\(V:\frac{1}{3}\pi r^2h=\frac{1}{3}\pi.3^2.4=12\pi\left(cm^3\right)\)
Diện tích mặt đáy là : \(\pi.3^2=9\pi(m^2)\)
Diện tích xung quanh là : \(S_{xq}=\pi rl=\pi.3.l=24\pi-9\pi=15\pi=>l=5(m)\)
Chiều cao của khối chóp là \(h=\sqrt{l^2-r^2}=\sqrt{5^2-3^2}=4(m)\)
Thể tích của hình nón là : \(V=\frac{1}{3}\pi r^2h=\frac{1}{3}\pi.3^2.4=12\pi(m^3)\)