Hai người thợ cùng làm công việc trong 16 giờ thì xong. Nếu người thứ nhất làm 3 giờ, người thứ hai làm 6 giờ thì họ làm được 1/4 công việc. Hỏi mỗi người làm một mình thì trong bao lâu làm xong công việc?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giả sử người thứ nhất cùng người thứ hai làm trong 3 giờ thì được:
1/16 x 3 = 3/16 (công việc)
Thời gian còn lại của người thứ hai là:
6 – 3 = 3 (giờ)
3 giờ của người thứ hai thì làm được:
1/4 – 3/16 = 1/16 (công việc)
1 giờ người thứ hai làm được:
1/16 : 3 = 1/48 (công việc)
1 giờ người thứ nhất làm được;
1/16 – 1/48 = 1/24 (công việc)
Thời gian một mình người thứ nhất làm xong công việc là:
1 : 1/24 = 24 (giờ)
Đáp số: 24 giờ.

Đáp án A
Gọi thời gian người thợ thứ nhất làm một mình xong việc là x(giờ) (x > 16)
Thời gian người thợ thứ hai làm một mình xong việc là y(giờ) (y > 16)
Suy ra trong thời gian 1 giờ người thợ thứ nhất làm được 1/x công việc
Trong thời gian 3 giờ người thợ thứ nhất làm được 3/x công việc
Trong thời gian 1 giờ người thợ thứ hai làm được 1/y công việc
Trong thời gian 6 giờ người thợ thứ hai làm được 6/y công việc
Hai người cùng làm trong 16 giờ thì xong việc, nên 1 giờ cả 2 người làm được 1/16 ta có phương trình:
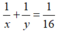
Người thứ nhất làm 3 giờ và người thứ hai làm 6 giờ thì được một phần tư công việc, ta có phương trình:
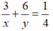
Từ đó ta có hệ phương trình:
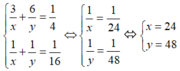
Kết luận: thời gian người thợ thứ nhất làm một mình xong việc là 24 (giờ)
Thời gian người thợ thứ hai làm một mình xong việc là 48 giờ

Hai người cùng làm trong \(3\)giờ thì được số phần công việc là:
\(3\div16=\frac{3}{16}\)(công việc)
Đổi: \(25\%=\frac{1}{4}\).
\(3\)giờ thì người thứ hai làm một mình được số phần công việc là:
\(\frac{1}{4}-\frac{3}{16}=\frac{1}{16}\)(công việc)
Mỗi giờ người thứ hai làm một mình được số phần công việc là:
\(\frac{1}{16}\div3=\frac{1}{48}\)(công việc)
Mỗi giờ người thứ nhất làm một mình được số phần công việc là:
\(\frac{1}{16}-\frac{1}{48}=\frac{1}{24}\)(công việc)
Người thứ nhất làm một mình thì xong công việc trong số giờ là:
\(1\div\frac{1}{24}=24\)(giờ)
Người thứ hai làm một mình thì xong công việc trong số giờ là:
\(1\div\frac{1}{48}=48\)(giờ)
Theo đề bài: Người thứ nhất làm 3 giờ và người thứ hai làm 6 giờ thì họ làm được 25% công việc.
Nên Người thứ nhất làm 24 giờ và người thứ hai làm 48 giờ thì họ làm được 200% công việc. Vậy:
Người thứ nhất làm xong công việc trong 24 giờ.
Người thứ hai làm xong công việc trong 48 giờ

Cả 2 người thợ làm cùng nhau mỗi giờ làm được
\(\dfrac{1}{4}+\dfrac{1}{6}=\dfrac{5}{12}\)( Công việc )
Cả 2 người thợ làm chung thì hoàn thành công việc sau
\(1:\dfrac{5}{12}=\dfrac{12}{5}=24h\)
Gọi thời gian người thứ nhất và người thứ hai hoàn thành công việc khi làm một mình lần lượt là x,y
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\\\dfrac{4}{x}+\dfrac{6}{y}=\dfrac{5}{12}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{24}\\\dfrac{1}{y}=\dfrac{1}{24}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=24\\y=24\end{matrix}\right.\)

một giờ cả hai người làm được:
1:16 =1/16 công việc
theo bài ra ,2 người cùng làm một công việc trong 16 giờ vậy 3 giờ cả hai người làm được:
3 nhân 1/16=3/16 cv
người thứ 2 làm được 25% tức là 1/4 cv
3 giờ người thứ hai lam được:
1/4:3=1/16 cv
một mình người thư hai làm được:
1:(1/16:3)=48 giờ
một mình người thứ 1 làm được:
1:(1/16-1/48)=24 giờ

Gọi thời gian người thứ nhất và người thứ hai hoàn thành công việc khi làm một mình lần lượt là x(giờ),y(giờ)
(Điều kiện: x>0 và y>0)
Trong 1 giờ, người thứ nhất làm được \(\dfrac{1}{x}\)(công việc)
Trong 1 giờ, người thứ hai làm được \(\dfrac{1}{y}\)(công việc)
Trong 1 giờ, hai người làm được \(\dfrac{1}{16}\left(côngviệc\right)\)
Do đó, ta có phương trình: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{16}\left(1\right)\)
Trong 15 giờ thì người thứ nhất làm được \(\dfrac{15}{x}\)(công việc)
Trong 6 giờ thì người thứ hai làm được \(\dfrac{6}{y}\)(công việc)
Nếu người thứ nhất làm trong 15 giờ và người thứ hai làm trong 6 giờ thì hai người làm được 75% công việc nên ta có:
\(\dfrac{15}{x}+\dfrac{6}{y}=75\%=\dfrac{3}{4}\)
=>\(\dfrac{5}{x}+\dfrac{2}{y}=\dfrac{1}{4}\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{16}\\\dfrac{5}{x}+\dfrac{2}{y}=\dfrac{1}{4}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{5}{x}+\dfrac{5}{y}=\dfrac{5}{16}\\\dfrac{5}{x}+\dfrac{2}{y}=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{y}=\dfrac{5}{16}-\dfrac{1}{4}=\dfrac{1}{16}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{16}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=48\\\dfrac{1}{x}=\dfrac{1}{16}-\dfrac{1}{48}=\dfrac{1}{24}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=24\\y=48\end{matrix}\right.\left(nhận\right)\)
Vậy: Để hoàn thành xong công việc khi làm một mình thì người thứ nhất cần 24 giờ, còn người thứ hai cần 48 giờ

Giả sử người thứ nhất cùng làm người thứ 2 làm trong 3 giờ thì được:
1/16 x 3 = 3/16 ( công việc )
Thời gian còn lại của người thứ hai là:
6 - 3 = 3 (giờ)
3 giờ của người thứ hai thì làm được:
1/4 - 3/16 = 1/16 (công việc)
1 giờ người thứ hai làm được:
1/16 : 3 = 1/48 (công việc)
1 giờ người thứ nhất làm được:
1/16 - 1/18 = 1/24 (công việc)
Thời gian 1 mình người thứ nhất làm xong công việc là:
1 : 1/24 = 24 (giờ)
Đ/s: 24 giờ
mình nhé!!!!!!!!Chúc bạn học tốt <3
24 giờ bạn ạ. Còn lời giải mình đăng lên sau nhá?