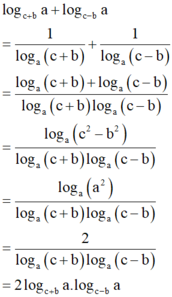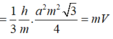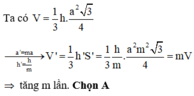Nếu độ dài hai cạnh góc vuông của tam giác vuông tăng lên 2 lần, 3 lần thì độ dài cạnh huyền thay đổi như thế nào? Mệnh đề tổng quát, với n∈N* còn đúng không?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi độ dài cạnh góc vuông nhỏ là x (m)(x > 0)
Độ dài cạnh góc vuông lớn là x + 8 (m)
Khi tăng độ dài cạnh góc vuông nhỏ lên 2 lần ta được cạnh có độ dài 2x (m)
Khi giảm độ dài cạnh góc vuông còn lại xuống 3 lần thì được cạnh có độ dài 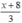 (m)
(m)
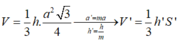
Tam giác vuông mới có diện tích bằng 51 m 2
Theo công thức tính diện tích tam giác vuông ta có phương trình:
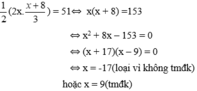
Vậy độ dài cạnh góc vuông nhỏ là 9m. Độ dài cạnh góc vuông lớn là 17m.

Đáp án B
Từ giả thiết ta có a 2 + b 2 = c 2
log c + b a + log c − b a = 1 log a c + b + 1 log a c − b = log a c + b + log a c − b log a c + b log a c − b = log a c 2 − b 2 log a c + b log a c − b = log a a 2 log a c + b log a c − b = 2 log a c + b log a c − b = 2 log c + b a . log c − b a

Xét mệnh đề
log c a + b + log c a - b = 2 ⇔ log c a + b a - b = 2 ⇔ a 2 - b 2 = c
(luôn đúng)
* Xét mệnh đề
log sin x 1 + cos x + log sin x 1 - cos x = 2 ⇔ log sin x 1 - cos 2 x = 2 ⇔ 1 - cos 2 x = sin 2 x
(luôn đúng).
Đáp án D

Đặt \(\frac{AB}{BC}=\frac{3}{5}=x\Rightarrow AB=3x;BC=5x\)
Tam giác ABC vuông tại A, theo py ta go:
\(AB^2+AC^2=BC^2\Rightarrow9x^2+144=25x^2\Rightarrow16x^2=144\Leftrightarrow x^2=9\)
=> X = 3 ; AB = 3x = 3.3=9 ; BC= 5x = 5.3 = 15
TAm giac ABC vuông tại A theo hệ thức lượng
AH.BC = AB.AC => AH= (AB.AC)/BC = (9.12)/15 = 7,2cm
AB^2 = BC . BH => BH = AB^2 /BC = 9^2/15 = 5,4
=> HC = BC - HB = 15 - 5,4 = 9,6cm
VẬY AH = 7,2 ; BH = 5,4;CH = 9,6

Trên tia Oy lấy điểm M/ sao cho OM/ = n thìNM/ = OM.
Vẽ tia phân giác Oz của góc xOy, vẽ đường trung trực OM/ cắt tia Oz
ở I, ta có OI = IM/, OIM/ cân tại I, do đó , mà nên .
OIM = IM/N (c.g.c) IM = IN. Vậy điểm I thuộc đường trung trực của MN.
Vì góc xOy cố định nên Oz cố định. M/OI mà OM/ = n không đổi nên điểm M/ cố định. Vì vậy đường trung trực của OM/ cố định nên điểm I cố định.
Vậy khi 2 điểm M và N thay đổi trên Ox, Oy sao cho OM + ON = n không đổi thì đường trung trực của đoạn MN luôn luôn đi qua điểm I cố định
NM/ = OM. Trên tia Oy lấy điểm M/ sao cho OM/ = n thì
Vẽ tia phân giác Oz của góc xOy, vẽ đường trung trực OM/ cắt tia Oz
ở I, ta có OI = IM/, OIM/ cân tại I, do đó , mà nên .
OIM = IM/N (c.g.c) IM = IN. Vậy điểm I thuộc đường trung trực của MN.
Vì góc xOy cố định nên Oz cố định. M/OI mà OM/ = n không đổi nên điểm M/ cố định. Vì vậy đường trung trực của OM/ cố định nên điểm I cố định.
Vậy khi 2 điểm M và N thay đổi trên Ox, Oy sao cho OM + ON = n không đổi thì đường trung trực của đoạn MN luôn luôn đi qua điểm I cố định.