1. Cho đường thẳng (đ): va \(y=\frac{-1}{2}x+2\)Parabol (P): \(y=\frac{1}{4}x^2\)trên hệ trục Oxy
a> Vẽ (P) vả (d) đã cho.
b) Goí A,B là giao điểm của (d) và (P). Tìm điểm N trên trục hoành sao cho tam giác NAB cân tại N.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ML
8 tháng 5 2018
a. Bạn tự vẽ nhé, dễ rồi !
b.
Vì A,B là 2 giao điểm của đt (d) với (P) => \(^{x_A,x_B}\)là nghiệm của pt hoành độ giao điểm sau:
\(-\frac{1}{2}x+2=\frac{1}{4}x^2\)
<=> \(\frac{1}{4}x^2+\frac{1}{2}x-2=0\)
<=> \(x^2+2x-8=0\)
<=> \(x^2+2x+1-9=0\)
<=> \(\left(x+1\right)^2-3^2=0\)
\(\Leftrightarrow\left(x+4\right)\left(x-2\right)=0\)
<=> \(\orbr{\begin{cases}x_A=-4\\x_{B=2}\end{cases}}\)
=> \(\hept{\begin{cases}A\left(-4;4\right)\\B\left(2;1\right)\end{cases}}\)
Điểm N thuộc trục hoành => N(n;0)
Ta có: \(NA=\sqrt{\left(x_A-x_N\right)^2+\left(y_A-y_N\right)^2}\)= \(\sqrt{\left(-4-n\right)^2+4^2}=\sqrt{n^2+8n+32}\)
\(NB=\sqrt{(x_B-x_N)^2+\left(y_B-y_N\right)^2}\)= \(\sqrt{\left(2-n\right)^2+1^2}=\sqrt{n^2-4n+5}\)
Tam giác NAB cân tại N <=> NA =NB <=> \(\sqrt{n^2+8n+32}=\sqrt{n^2-4n+5}\)
<=> \(n^2+8n+32=n^2-4n+5\)
<=> \(n=\frac{-27}{12}=\frac{-9}{4}\)
=> \(N\left(\frac{-9}{4};0\right)\)
SS
13 tháng 3 2022
a)Hoành độ giao điểm của (P)và (d) là:
\(\frac{1}{2}x^2=x+4\)
\(\Leftrightarrow x^2=2x+8\)
\(\Leftrightarrow x^2-2x-8=0\)
\(\Leftrightarrow\left(x+2\right).\left(x-4\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+2=0\\x-4=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-2\\x=4\end{cases}}}\)
Thay \(x=-2\)vào (d) ta được:
\(y=-2+4=2\)
Thay \(x=4\)vào (d)ta được:
\(y=4+4=8\)
Vậy \(A\left(-2;2\right),B\left(4;8\right)\)hoặc \(A\left(4;8\right),B\left(-2;2\right)\)
b)Mk ko bt làm
31 tháng 8 2021
b: Phương trình hoành độ giao điểm là:
\(-\dfrac{1}{2}x^2=-\dfrac{1}{2}x-1\)
\(\Leftrightarrow-\dfrac{1}{2}x^2+\dfrac{1}{2}x+1=0\)
\(\Leftrightarrow x^2-x-2=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
Thay x=2 vào (P), ta được:
\(y=\dfrac{-2^2}{2}=-2\)
Thay x=-1 vào (P), ta được:
\(y=-\dfrac{1^2}{2}=-\dfrac{1}{2}\)
31 tháng 3 2021
b) Phương trình hoành độ giao điểm của (P) và (d) là:
\(x^2=x+2\)
\(\Leftrightarrow x^2-x-2=0\)
\(\Leftrightarrow x^2-2x+x-2=0\)
\(\Leftrightarrow x\left(x-2\right)+\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
Thay x=2 vào (P), ta được:
\(y=2^2=4\)
Thay x=-1 vào (P), ta được:
\(y=\left(-1\right)^2=1\)
Vậy: A(2;4) và B(-1;1)
26 tháng 3 2023
a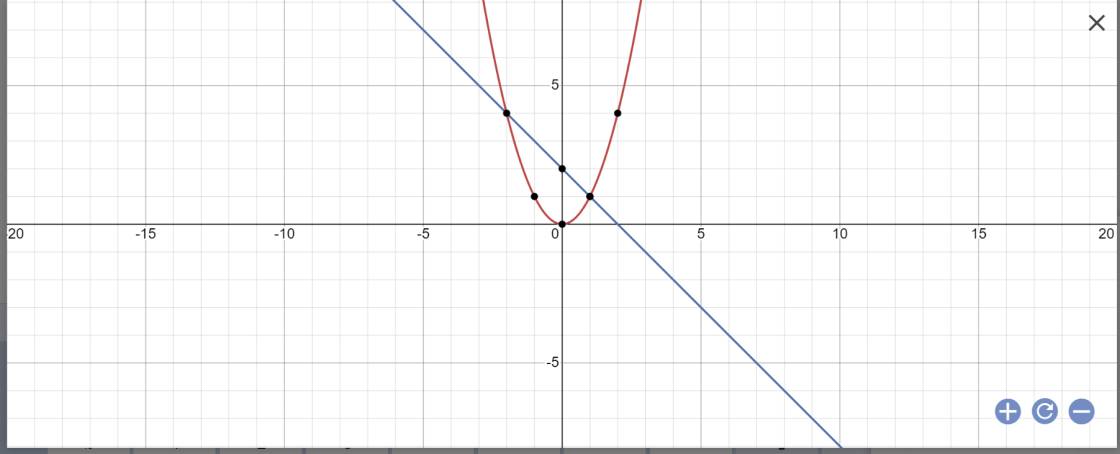
b:
PTHĐGĐ là:
x^2+x-2=0
=>(x+2)(x-1)=0
=>x=-2 hoặc x=1
=>y=4 hoặc y=1
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
17 tháng 11 2023
a/ bạn tự làm
b/ \(\Rightarrow y=0\Rightarrow\dfrac{1}{2}x+2=0\) giải PT tìm hoành độ x
c/ \(\Rightarrow x=0\Rightarrow y=0+2=2\)
d/ \(\Rightarrow\dfrac{1}{2}x+2=-x+2\) Giải PT tìm hoành độ x của C rồi thay vào d1 hoặc d2 để tìm tung độ y của C