3 cầu thủ sút phạt đền 11m , mỗi người đá 1 lần với xác suất ghi bàn tương ứng là 0,85;0,6 và 0,5 . tính xác suất để
a Có đúng 1 cầu thủ ghi bàn
b Có ít nhất 1 người ghi bàn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 1 2023
\(Xác\text{ }suất\text{ }ít\text{ }nhất\text{ }để\text{ }một\text{ }trong\text{ }ba\text{ }cầu\text{ }thủ\text{ }gi\text{ }bàn\text{ }là:\)
\(1-\left(1-x\right)\left(1-y\right)\cdot0,4=0,976_{\left(1\right)}\)
\(Xác\text{ }suất\text{ }để\text{ }cả\text{ }ba\text{ }cầu\text{ }thủ\text{ }đều\text{ }ghi\text{ }bàn\text{ }là:\)
\(0,6xy=0,336\Leftrightarrow xy=56\Leftrightarrow y=\dfrac{0,56}{x}_{\left(2\right)}\)
\(Thay_{\left(2\right)}vào_{\left(1\right)}ta\text{ }có:\)
\(1-\left(1-x\right)\left(1-\dfrac{0,56}{x}\right)\cdot0,4=0,976\)
\(\Leftrightarrow\left(1-\dfrac{0,56}{x}-x+0,56\right)\cdot0,4=0,24\)
\(\Leftrightarrow1,56-\dfrac{0,56}{x}-x=0,06\)
\(\Leftrightarrow\dfrac{0,56}{x}+x=1,5\Leftrightarrow x^2-1,5x+0,56=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0,7\Rightarrow y=0,8\left(ktm\right)\\x=0,8\Rightarrow y=7\left(tm\right)\end{matrix}\right.\)
\(Xác\text{ }suất\text{ }để\text{ }có\text{ }đúng\text{ }hai\text{ }cầu\text{ }thủ\text{ }ghi\text{ }bàn\text{ }là:\\ 0,8\cdot0,7\cdot0,4+0,8\cdot0,3\cdot0,6+0,2\cdot0,7\cdot0,6=0,452\)
CM
18 tháng 11 2019
Chọn đáp án A
Gọi Ai là biến cố “cầu thủ thứ I ghi bàn” với i ∈ 1 ; 2 ; 3 .
Các biến cố Ai độc lập với nhau và P(A1) = x; P(A2) = y; P(A3) = 0,6.
* Gọi A là biến cố “Có ít nhất một trong ba cầu thủ ghi bàn” P(A) = 0,976.
Ta có là biến cố “không có cầu thủ nào ghi bàn”.
Ta có phương trình
* Gọi B là biến cố “Cả ba cầu thủ đều ghi bàn” P(B) = 0,336.
Mặt khác P(B) = P(A1).P(A2).P(A3) = 0,6xy.
Ta có phương trình
* Từ (1) và (2) ta có hệ phương trình
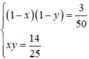
Suy ra x, y là nghiệm của phương trình
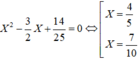
Do x > y nên x = 4 5 = 0 , 8 và y = 7 10 = 0 , 7 .
* Gọi C là biến cố “Có đúng hai cầu thủ ghi bàn”
Khi đó
⇒ P C = 0 , 452
11 tháng 10 2015
CÓ ÍT NHẤT 1 cầu thủ ghi bàn có 2 cách làm
cách thứ nhất:
có ít nhất 1 cầu thủ ghi bàn có 3 trường hợp xảy ra là: cầu thủ 1 ghi bàn cầu thủ 2 không ghi bàn, cầu thủ 2 ghi bàn cầu thủ 1 không ghi bàn, và cả 2 cầu thủ ghi bàn
suy ra sx bằng: 0.8.0,3+0,7.0,2+0,7.,8
cách thứ 2 là : sử dụng biến cố đối
A: không có cầu thủ nào ghi bàn
với P(A)=0,2.0,3
B" có ít nhất 1 cầu thủ ghi bàn"
P(B)=1-P(A)=1-0,2.0,3
CM
10 tháng 11 2019
Gọi A là biến cố cầu thủ thứ nhất ghi bàn
B là biến cố cầu thủ thứ hai ghi bàn
X là biến cố ít nhất 1 trong hai cầu thủ ghi bàn
Suy ra: X ¯ = A ¯ . B ¯
Vì hai biến cố A ¯ ; B ¯ độc lập với nhau nên ta có:
P ( X ¯ ) = P ( A ¯ ) . P ( B ¯ ) = ( 1 − 0 , 8 ) . ( 1 − 0 , 7 ) = 0 , 06
Do đó, xác suất để có ít nhất 1 trong hai cầu thủ ghi bàn là:
P ( X ) = 1 − P ( X ¯ ) = 1 − 0 , 06 = 0 , 94
Chọn đáp án B
CM
15 tháng 2 2017
Đáp án B
Gọi A là biến cố “Cú sút đó không vào lưới”. Nếu cầu thủ sút vào vị trí 1 hoặc 2, xác suất để bóng không vào bằng 2 1 4 . 1 4 = 1 8 . Nếu cầu thủ sút cào vị trí 3 hoặc 4, xác suất để bóng không vào bằng 2 1 4 . 1 4 . 1 2 = 1 16 . Suy ra xác suất để bóng không vào bằng P A = 1 8 + 1 16 = 3 16 .
CM
13 tháng 10 2017
Đáp án B
Gọi A là biến cố “Cú sút đó không vào lưới”. Nếu cầu thủ sút vào vị trí 1 hoặc 2, xác suất để bóng không vào bằng 2 . 1 4 . 1 4 = 1 8 . Nếu cầu thủ sút cào vị trí 3 hoặc 4, xác suất để bóng không vào bằng 2 . 1 4 . 1 4 . 1 2 = 1 16 . Suy ra xác suất để bóng không vào bằng P ( A ) = 1 8 + 1 16 = 3 16 .
15 tháng 5 2022
số lần Xuân Trường sút thành công là:
50 x 80% = 40 (lần)
số lần Văn Toàn sút thành công là:
60 x 95% = 57 (lần)
tổng số lần sút thành công của 2 cầu thủ là:
40 + 57 = 97 (lần)
đáp số: 97 lần
15 tháng 5 2022
Tham khảo
80% của 50 là 40.
95% của 60 là 57.
40+57=97 (lần).
Vậy hai cầu thủ Xuân Trường và Văn Toàn sút thành công tổng cộng 97 lần.
Xác suất ghi bàn tương ứng là 0,85; 0,6 và 0,5 đồng nghĩa xác suất đá trượt tương ứng là 0,15; 0,4 và 0,5
a. Có đúng 1 cầu thủ ghi bàn (nghĩa là 2 cầu thủ còn lại đá trượt): (gồm các TH1: (cầu thủ 1 ghi bàn, cầu thủ 2 đá trượt, cầu thủ 3 đá trượt); TH2: cầu thủ 1 đá trượt, cầu thủ 2 ghi bàn, cầu thủ 3 đá trượt; TH3: cầu thủ 1 đá trượt, cầu thủ 2 đá trượt, cầu thủ 3 ghi bàn):
\(P=0,85.0,4.0,5+0,15.0,6.0,5+0,15.0,4.0,5=...\)
b. Ta sẽ sử dụng quy tắc loại trừ (hay còn gọi là phần bù) để làm câu này.
Tổng xác suất của: "có ít nhất 1 người ghi bàn" và "tất cả đều đá trượt" bằng 1
Do đó, ta chỉ cần tìm xác suất của "tất cả đều đá trượt" rồi lấy 1 trừ đi là được.
Xác suất để tất cả đều đá trượt:
\(\overline{P}=0,15.0,4.0,5=...\)
Xác suất cần tìm: \(P=1-\overline{P}=...\)