dùng đồ thị hàm số chứng minh bất đẳng thức
\(\sqrt{x^2-4x+4}>x-3\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PP
1
1 tháng 7 2018
VP=√(x^2-4x+4)=|x-2|
dt hai nua dt (d1): y=2-x; (x<2);
(d2): y=x-2 (x≥2)
VT: (d3): y=x-3
(d3) nam phia duoi (d1) &(d2) =>VT>VP=>dpcm
HN
0
I
2
WR
30 tháng 6 2019
\(\frac{x^2+5}{\sqrt{x^2+4}}=\sqrt{x^2+4}+\frac{1}{\sqrt{x^2+4}}\ge2.\)(BĐT Cauchy)
Dấu "=" xra khi \(\sqrt{x^2+4}=\frac{1}{\sqrt{x^2+4}}\Leftrightarrow x^2+4=1\left(vl\right)\)
Dấu "=" ko xra=>đpcm
30 tháng 6 2019
Witch Rose: Dùng luôn AM-GM dưới mẫu cũng được mà.
\(\frac{x^2+5}{\sqrt{x^2+4}}=\frac{x^2+5}{\sqrt{x^2+4}.1}\ge\frac{x^2+5}{\frac{x^2+5}{2}}=2\)
Dấu " = " xảy ra <=> \(1=x^2+4\)( vô lý )
=> đpcm
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 7 2021
\(y=\left|x+1\right|+\sqrt{\left(x-2\right)^2}=\left|x+1\right|+\left|x-2\right|\)
\(\Rightarrow\left\{{}\begin{matrix}y=2x-1\text{ với }x\ge2\\y=1-2x\text{ với }x\le-1\\y=3\text{ với }-1\le x\le2\end{matrix}\right.\)
Từ đó ta có đồ thị hàm số như sau (vẽ 3 đồ thị hàm bậc nhất xác định trên trên ở từng khoảng của chúng)
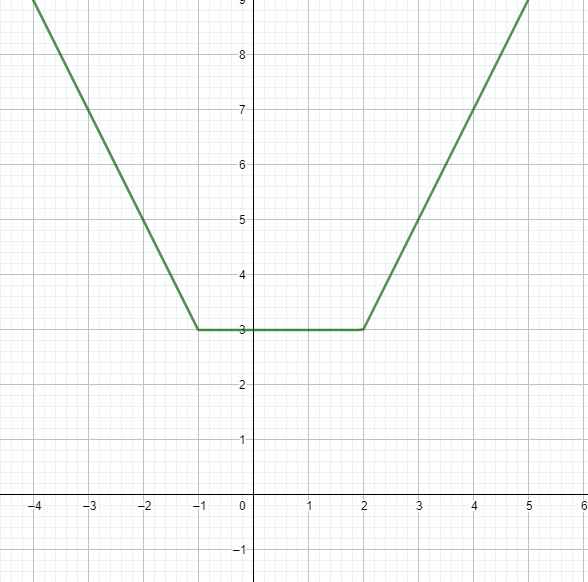
Từ đồ thị \(\Rightarrow y_{min}=3\) khi \(-1\le x\le2\)
TL
3
PT
2 tháng 11 2019
Một cửa hàng ngày đầu bán được 3 tạ 16 kg gạo, ngày sau bán được hơn ngày đầu 3,5 yến. Hỏi cả hai ngày bán đươc bao nhiêu tạ gạo ?
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 7 2021
\(y=\sqrt{\left(2x-1\right)^2}+\sqrt{\left(x-2\right)^2}=\left|2x-1\right|+\left|x-2\right|\)
\(y=\left[{}\begin{matrix}3x-3\left(\text{với }x\ge2\right)\\3-3x\left(\text{với }x\le\dfrac{1}{2}\right)\\x+1\left(\text{với }\dfrac{1}{2}\le x\le2\right)\end{matrix}\right.\)
Từ đó ta có đồ thị hàm số như sau:
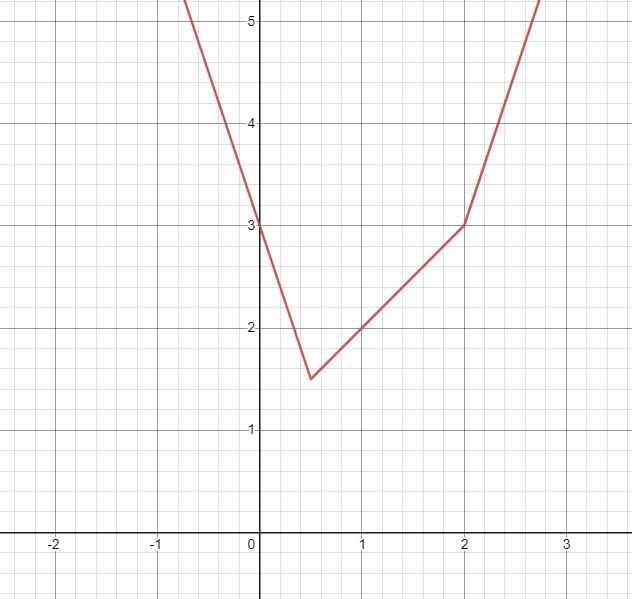
Từ đồ thị ta thấy phương trình \(\sqrt{4x^2-4x+1}+\sqrt{x^2-4x+4}=m\):
- Có đúng 1 nghiệm khi \(m=\dfrac{3}{2}\)
- Có 2 nghiệm phân biệt khi \(m>\dfrac{3}{2}\)
- Vô nghiệm khi \(m< \dfrac{3}{2}\)
\(\sqrt{x^2-4x+4}=\sqrt{\left(x-2\right)^2}=|x-2|\)
x - 2 > x - 3