Một ô tô đi quãng đường AB dài 80 km trong một thời gian đã định. 3/4 quãng đường đầu ô tô chạy nhanh hơn dự định 10 km/h, quãng đường còn lại ô tô chạy chậm hơn dự định 15 km/h. Biết rằng ô tô đến B đúng giờ qui định. Tính thời gian ô tô đi hết quãng đường AB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TH
18 tháng 1 2018
Ta đặt v (km/h) là vận tốc sẽ dự định đi.
Trong 3/4 quãng đường ban đầu tức 60km đầu: otô chạy nhanh hơn dự định 10km/h => vận tốc lúc đầu là v+10 (km/h)
Trong quãng đg còn lại tức 20km cuối: oto chạy chậm hơn dự định 15km/h => vận tốc lúc sau là v-15 (km/h)
Do oto về đến B đúng giờ quy định, ta có phương trình:
60/(v+10) + 20/(v-15) = 80/v
Qui đồng mẫu số, ta có:
60*v*(v-15) + 20*v*(v+10) = 80*(v+10)*(v-15)
Khai triển ra rồi rút gọn, ta đc phương trình:
300*v = 12000
=> v = 40 (km/h)
Vậy thời gian oto đi hết quãng đg AB là:
v = AB/t
=> t = AB/v = 80/40 = 2 (h)
KL: Thời gian oto đi hết quãng đg AB là 2h
TH
18 tháng 1 2018
Trả lời:
Ta đặt v (km/h) là vận tốc sẽ dự định đi.
Trong 3/4 quãng đường ban đầu tức 60km đầu: otô chạy nhanh hơn dự định 10km/h => vận tốc lúc đầu là v+10 (km/h)
Trong quãng đg còn lại tức 20km cuối: oto chạy chậm hơn dự định 15km/h => vận tốc lúc sau là v-15 (km/h)
Do oto về đến B đúng giờ quy định, ta có phương trình:
60/(v+10) + 20/(v-15) = 80/v Qui đồng mẫu số, ta có:
60*v*(v-15) + 20*v*(v+10) = 80*(v+10)*(v-15)
Khai triển ra rồi rút gọn, ta đc phương trình:
300*v = 12000
=> v = 40 (km/h)
Vậy thời gian oto đi hết quãng đg AB là:
v = AB/t
=> t = AB/v = 80/40 = 2 (h)
KL: Thời gian oto đi hết quãng đg AB là 2h
CM
18 tháng 5 2019
Gọi vận tốc ô tô dự định đi là v (km/h), (v > 3)
Thời gian đi 75 km đường đầu là 75/(v+2) (h)
Thời gian đi 120 – 75 = 45 km còn lại là 45/(v-3) (h)
Vì xe đến đũng thời gian dự định nên ta có phương trình:
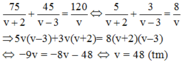
Vậy thời gian dự định là 120/48 = 2,5 giờ
Đáp án: A
CM
6 tháng 7 2017
Gọi vận tốc ô tô dự định đi quãng đường AB là x (km/h).
Có phương trình: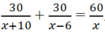 
Giải ra được x = 30
Thời gian ô tô dự định đi là 2 giờ.
27 tháng 3 2020
Gọi vận tốc dự định là \(x\left(km/h\right)x>6\)
Thực tế \(\left(x-6\right),\left(x+12\right)\)
Thời gian dự định \(t=\frac{80}{x}\)
Thời gian thực tế \(\frac{40}{\left(x-6\right)}+\frac{40}{\left(x+12\right)}\)
Ta có pt: \(\frac{80}{x}=\frac{40}{\left(x-6\right)}+\frac{40}{\left(x+12\right)}\)
\(\Leftrightarrow x=24\)
Vận tốc dự định là \(24km/h\)
CM
5 tháng 4 2017
Gọi vận tốc ô tô dự định là v (km/h), (v > 6)
Thời gian đi nửa quãng đường đầu là 30/(v+10) (h)
Thời gian đi nửa quãng đường sau là 30/(v-6) (h)
Thời gian dự định đi quãng đường AB là 60/v (h)
Theo bài ra ta có:
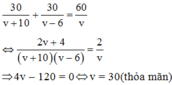
Vậy thời gian dự định là 60/30 = 2 giờ
Đáp án: B
9 tháng 4 2020
Vận tốc dự định là x ( km/h )
Thời gian dự định là 7 ( h )
Quãng đường là xy ( km)
*) Mỗi giờ chậm hơn 10km => ( x - 10 ) km / h
=> t = \(\frac{xy}{\left(x-10\right)}=y-\frac{4}{5}\)
*) Mỗi giờ chậm hơn 20 km
t=\(\frac{xy}{x-20}=y-2\)
<=>\(\hept{\begin{cases}xy=\left(x-20\right)\left(y-2\right)\\5xy=\left(5y-4\right)\left(x-10\right)\end{cases}}\)
<=> \(\hept{\begin{cases}xy=xy-2x-20y+40\\5xy=5xy-50y-4x+40\end{cases}}\)
<=> \(\hept{\begin{cases}2x+20y=40\\50y+4x=40\end{cases}}\)
<=> \(\hept{\begin{cases}x=60\\y=4\end{cases}}\)
DK
3 tháng 2 2021
Đáp án:
Vận tốc dự định của ô tô là 60km/h, quãng đường AB là 240km
Giải thích các bước giải:
Đổi : $48'=\dfrac{4}{5}h
Gọi vận tốc dự định của ô tô đi từ A đếnB là x (km/h) (x>0)
Thời gian dự định của xe đi từ A đến B là y (h) (y>0)
Nếu xe chạy mỗi giờ chậm hơn 10km thì đến B chậm hơn 4545 h khi đó:
Vận tốc của xe là x-10 (km/h)
Thời gian đi của xe là y+4545 (h)
⇒⇒ Độ dài quãng đường là (x−10)(y+45)(x−10)(y+45) (km)
⇒⇒ Ta có pt: (x−10)(y+45)=xy(x−10)(y+45)=xy
↔45x−10y=8⇔4x−50y=40↔45x−10y=8⇔4x−50y=40 (1)
Nếu xe mỗi giờ chạy chậm 20 km thì đến chậm hơn 2h khi đó:
Vận tốc của xe là x-20 (km/h)
Thời gian đi của xe là y+2 (h)
⇒⇒ Độ dài quãng đường là (x-20)(y+2) (km)
⇒⇒ Ta có pt: (x−20)(y+2)=xy(x−20)(y+2)=xy
⇔2x−20y=40⇔x−10y=20⇔2x−20y=40⇔x−10y=20 (2)
Ta có hệ phương trình (1) và (2)
(2) ⇒x=20+10y⇒x=20+10y thay vào (1) ta được:
4(20+10y)−50y=40⇒y=4⇒x=60⇒4(20+10y)−50y=40⇒y=4⇒x=60⇒ quãng đường AB là 4.60=240km4.60=240km
Vậy vận tốc dự định của ô tô là 60km/h và quãng đường AB là 240km.
CM
1 tháng 12 2018
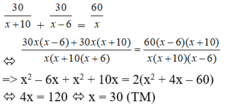
Vậy thời gian dự định đi quãng đường AB là 60 : 30 = 2 giờ
Đáp án cần chọn là D
2h bạn nhé!!
Bài giải
Gọi vận tốc dự định đi là x. Thời gian dự kiến đi trên đoạn AB là \(\frac{80}{x}\)
\(\frac{3}{4}\) quãng đường dài: 3/4 x 80 = 60 km
\(\frac{1}{4}\)quãng đường còn lại là: \(\frac{1}{4}\) x 80 = 20km.
Theo bài ra: 60 km đầu xe đi với vận tốc x + 10 => Thời gian đi 60km đầu là: \(\frac{60}{\left(x+10\right)}\)
20 km sau ô tô đi với vận tốc x - 15 => Thời gian đi 20km là: \(\frac{20}{\left(x-15\right)}\)
Vì ô tô đến B đúng giờ qui định nên ta có phương trình:
\(\frac{60}{x+10}+\frac{20}{x-15}=\frac{80}{x}\)
Giải phương trình trên ta tìm được x = 40 (km/h)
Thời gian ô tô đi hết quãng đường AB là:
80 : 40 = 2 (giờ)
Đáp số : 2 giờ