Cho hình vuông ABCD cạnh a. Gọi D là đường thẳng bất kì đi qua giao điểm O của hai đường chéo. Gọi A', B', C', D' lần lượt là chân các đường vuông góc kẻ từ A, B, C, D đến đường thẳng d.
Chứng minh tổng A'A2 + B'B2 + C'C2 + D'D2 không đổi khi d quay xung quanh điểm O.



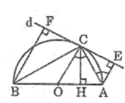
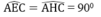
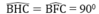
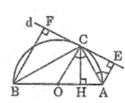
Đặt độ dài mối cạnh của hình vuông là a (a\(\in\)R+)
Ta thấy:\(\Delta\)AA'O vuông tại A' => ^A'AO + A'OA = 900
Mà ^A'OA + ^B'OB = 900 nên ^A'AO = ^B'OB
Xét \(\Delta\)AA'O và \(\Delta\)OB'B: ^AA'O = ^OB'B = 900; AO=BO; ^A'AO = ^B'OB
=> \(\Delta\)AA'O = \(\Delta\)OB'B (Cạnh huyền góc nhọn) => AA'=OB'
Xét \(\Delta\)BB'O: ^BB'O=900 => OB' 2 + BB' 2 = OB2
Do AA' = OB' => AA' 2 + BB' 2 = OB2 (1)
Tương tự, ta có: CC' 2 + DD' 2 = OC2 (2)
Cộng (1) với (2) => AA' 2 + BB' 2 + CC' 2 + DD' 2 = OB2 +OC2 = a2 (Vì \(\Delta\)BOC vuông cân đỉnh O)
Mà a không đổi nên ta có điều phải chứng minh.