Question

[gấukoala]

Tính \(\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\)

jjjjjjjjjjjjjhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhh                                                                                                                                                                                                                                                    

Answer 1

[Nguyễn Huy Tú]

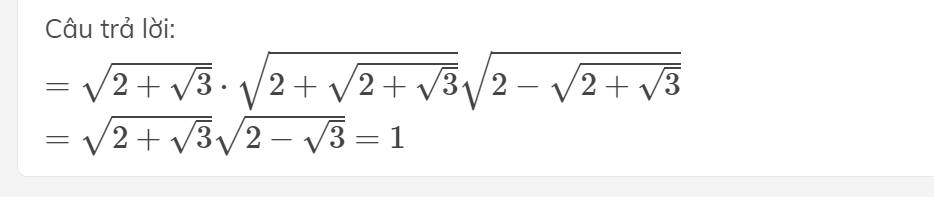
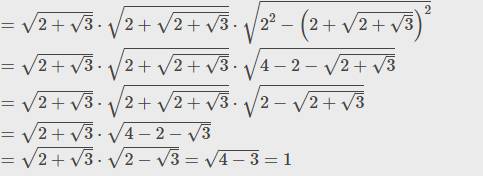
Đặt \(A=\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\)

\(\sqrt{2}A=\sqrt{4-2\sqrt{3}}-\sqrt{4+2\sqrt{3}}\)

\(=\sqrt{\left(\sqrt{3}-1\right)^2}-\sqrt{\left(\sqrt{3}+1\right)^2}=\left|\sqrt{3}-1\right|-\left|\sqrt{3}+1\right|\)

\(=\sqrt{3}-1-\sqrt{3}-1=-2\)

Vậy \(\Rightarrow A=\frac{-2}{\sqrt{2}}=-\sqrt{2}\)