Cho điểm A nằm ngoài đường tròn (O;R). Từ A kẻ đường thắng d bất kì không đi qua điểm O va cắt (O) tại B,C(AB<AC). Các tiếp tuyến của (O) tại B và C cắt nhau tại D. Kẻ DH vuông góc AO tại H. DH cắt cung nhỏ BC tại M. Gọi I là giao điểm của DO và BC.
1, CM:5 điểm D,H,B,O,C cùng thuộc 1 đường tròn và tứ giác DIHA nội tiếp.
2,CM:AM là tiếp tuyến của (O)
3, CM: HB.HC không đổi khi d quay quanh A






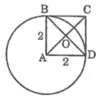
O A B D C I H M d
1) Do DB và DC là 2 tiếp tuyến của (O) => ^DBO=^DCO=900
=> Tứ giác DBOC nội tiếp đường tròn (Tâm là trung điểm OD) (1)
Xét tứ giác DHOC: ^DHO=^DCO=900
=> Tứ giác DHOC nội tiếp đường tròn (Tâm là trung điểm DO) (2)
Từ (1) và (2) => 5 điểm D,H,B,O,C cùng nằm trên 1 đường tròn (đpcm)
DB và DC là 2 tiếp tuyến của (O) => DB=DC => D thuộc trung trực của BC
Mà BC là dây cung của (O) nên O cũng thuộc trung trực của BC
=> OD \(\perp\)BC (tại I) => ^DIA=900
Xét tứ giác DIHA: ^DHA=^DIA=900 (cmt) => Tứ giác DIHA nội tiếp đường tròn (đpcm).
2) Dễ chứng minh \(\Delta\)OBI ~ \(\Delta\)ODB (g.g) => \(\frac{OB}{OD}=\frac{OI}{OB}\Rightarrow OB^2=OI.OD\)
Mà OB=OM (cùng nằm trên (O)) => \(OM^2=OI.OD\)(3)
Hoàn toàn c/m được \(\Delta\)OHD ~ \(\Delta\)OIA (g.g) => \(\frac{OH}{OI}=\frac{OD}{OA}\Rightarrow OH.OA=OI.OD\)(4)
Từ (3) và (4) => \(OM^2=OH.OA\)=> \(\frac{OM}{OA}=\frac{OH}{OM}\)
Xét \(\Delta\)OHM và \(\Delta\)OMA: \(\frac{OM}{OA}=\frac{OH}{OM}\); ^MOA chung => \(\Delta\)OHM ~ \(\Delta\)OMA (c.g.c)
=> ^OHM=^OMA. Ta có ^OHM=900 => ^OMA=900 => AM là tiếp tuyến của (O) (đpcm).
3) Ta có 5 điểm B,H,D,O,C cùng thuộc 1 đường tròn (cmt)
Suy ra Tứ giác BHOC và tứ giác DHOC nội tiếp đường tròn
Tứ giác BHOC nội tiếp đg tròn => ^ABH=^COH (Cùng bù ^HBC)
Dễ thấy ^BAH=^HDO (Cùng phụ ^DOA) (5)
Do tứ giác DHOC nôi tiếp đg tròn => ^HDO=^OCH (6)
Từ (5); (6) => ^BAH=^OCH
Xét \(\Delta\)AHB và \(\Delta\)CHO: ^ABH=^COH; ^BAH=^OCH => \(\Delta\)AHB ~ \(\Delta\)CHO (g,g)
\(\Rightarrow\)\(\frac{HB}{HO}=\frac{AH}{HC}\Rightarrow HB.HC=AH.HO\)(7)
Nhận thấy Đường tròn (O) có tiếp tuyến AM cố định (Do A cố định)
Mà MH\(\perp\)AO tại H => H cố định => AH và HO có giá trị không đổi
Nên AH.HO không đổi (8)
Từ (7) và (8) => HB.HC không đổi khi d quay quanh A (đpcm).