bình phương của hiệu 2 nghiệm bằng 13 ghi sao đc? (x1,x2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 5 2018
Đáp án B
P T ⇔ 2 2 x 2 − 5 2 x + 2 = 0 ⇔ 2 x = 2 2 x = 1 2 ⇔ x = 1 x = − 1 ⇒ x 1 = − 1 x 2 = 1 ⇒ x 2 − x 1 = 2.
17 tháng 4 2023
a: Khi m=1 thì (1): x^2-2(1-2)x+1^2-5-4=0
=>x^2+2x-8=0
=>(x+4)(x-2)=0
=>x=2 hoặc x=-4
b: Δ=(2m-4)^2-4(m^2-5m-4)
=4m^2-16m+16-4m^2+20m+16
=4m+32
Để pt có hai nghiệm phân biệt thì 4m+32>0
=>m>-8
x1^2+x2^2=-3x1x2-4
=>(x1+x2)^2+x1x2+4=0
=>(2m-4)^2+m^2-5m-4+4=0
=>4m^2-16m+16+m^2-5m=0
=>5m^2-21m+16=0
=>(m-1)(5m-16)=0
=>m=16/5 hoặc m=1
CM
11 tháng 11 2018
a) Xét: x2 - 4mx + 9.(m – 1)2 = 0 (1)
Δ’ = (2.m)2 – 9.(m – 1)2 = 4m2 – 9.(m2 – 2m + 1) = -5m2 + 18m – 9
Phương trình (1) có nghiệm ⇔ Δ’ ≥ 0
⇔ -5m2 + 18m – 9 ≥ 0
⇔ 5m2 - 18m + 9 ≤ 0
⇔ (5m – 3)(m – 3) ≤ 0
⇔ 3/5 ≤ m ≤ 3.
b) + x1 ; x2 là hai nghiệm của (1) nên theo định lý Vi-et ta có:
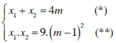
+ Tìm hệ thức giữa x1 và x2 không phụ thuộc vào m.
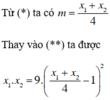
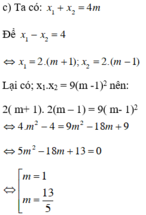
Thử lại:
+ m = 1, (1) trở thành x2 – 4x = 0 có hai nghiệm x = 0; x = 4 có hiệu bằng 4
+ m = 13/5, (1) trở thành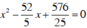 
có hai nghiệm x = 7,2 và x = 3,2 có hiệu bằng 4.
Vậy m = 1 hoặc m = 13/5.
HP
16 tháng 1 2021
Hình như đề thiếu, pt: \(x^2-\left(m+1\right)x+m-2=0\)
Phương trình đã cho có nghiệm khi \(\Delta=\left(m+1\right)^2-4\left(m-2\right)=m^2-2m+9>0\)
\(\Rightarrow\) Phương trình đã cho luôn có hai nghiệm phân biệt với mọi giá trị m
Định lí Viet: \(\left\{{}\begin{matrix}x_1+x_2=m+1\\x_1x_2=m-2\end{matrix}\right.\)
a, Theo giả thiết ta có: \(x_1^2+x_2^2=100\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=100\)
\(\Leftrightarrow\left(m+1\right)^2-2\left(m-2\right)=100\)
\(\Leftrightarrow m^2+2m+1-2m+4=100\)
\(\Leftrightarrow m^2=95\)
\(\Leftrightarrow m=\sqrt{95}\)
b, \(P=\left|x_1-x_2\right|\)
\(P^2=\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2\)
\(=\left(m+1\right)^2-4\left(m-2\right)\)
\(=m^2-2m+9=\left(m-1\right)^2+8\ge8\)
\(\Rightarrow P=\left|x_1-x_2\right|\ge2\sqrt{2}\)
\(minP=2\sqrt{2}\Leftrightarrow m=1\)
15 tháng 1 2022
\(\text{Δ}=\left(2m-6\right)^2-4\left(m^2+3m+2\right)\)
\(=4m^2-24m+36-4m^2-12m-8=-36m+28\)
Để phương trình có hai nghiệm thì -36m+28>=0
=>-36m>=-28
hay m<=7/9
Theo đề, ta có:
\(\left(x_1+x_2\right)^2-2x_1x_2=100\)
\(\Leftrightarrow\left(\dfrac{2m-6}{m+1}\right)^2-2\cdot\dfrac{m+2}{m+1}=100\)
\(\Leftrightarrow\dfrac{\left(2m-6\right)^2-2\left(m^2+3m+2\right)}{\left(m+1\right)^2}=100\)
\(\Leftrightarrow4m^2-24m+36-2m^2-6m-4=100\left(m+1\right)^2\)
\(\Leftrightarrow50\left(m+1\right)^2=m^2-15m+16\)
\(\Leftrightarrow50m^2+100m+50-m^2+15m-16=0\)
\(\Leftrightarrow49m^2+115m+34=0\)
\(\text{Δ}=115^2-4\cdot49\cdot34=6561\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}m_1=\dfrac{-115-81}{2\cdot49}=-2\left(nhận\right)\\m_2=\dfrac{-115+81}{2\cdot49}=-\dfrac{17}{49}\left(nhận\right)\end{matrix}\right.\)
Y
5 tháng 6 2023
\(x^2-\left(2m+1\right)x+m^2+1=0\)
\(\Delta=b^2-4ac=\left[-\left(2m+1\right)\right]^2-4\left(m^2+1\right)\)
\(=\left(4m^2+4m+1\right)-4m^2-4\)
\(=4m-3\)
Để pt có 2 nghiệm phân biệt \(x_1,x_2\) thì \(\Delta>0\Leftrightarrow4m-3>0\Leftrightarrow4m>3\Leftrightarrow m>\dfrac{3}{4}\)
Theo Vi ét, ta có : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m+1\\x_1x_2=\dfrac{c}{a}=m^2+1\end{matrix}\right.\)
Ta có : \(\left(x_1+1\right)^2+\left(x_2+1\right)^2=13\)
\(\Leftrightarrow x_1^2+2x_1+1+x_2^2+2x_2+1=13\)
\(\Leftrightarrow\left(x_1^2+x_1^2\right)+\left(2x_1+2x_2\right)+2=13\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2+2\left(x_1+x_2\right)-11=0\)
\(\Leftrightarrow\left(2m+1\right)^2-2\left(m^2+1\right)+2\left(2m+1\right)-11=0\)
\(\Leftrightarrow4m^2+4m+1-2m^2-2+4m+2-11=0\)
\(\Leftrightarrow2m^2+8m-10=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=1\left(tm\right)\\m=-5\left(ktm\right)\end{matrix}\right.\)
Vậy m = 1 thì thỏa mãn đề bài.
KV
5 tháng 6 2023
∆ = [-(2m + 1)]² - 4.1.(m² + 1)
= 4m² + 4m + 1 - 4m² - 4
= 4m - 3
Phương trình có hai nghiệm phân biệt khi ∆ > 0
⇔ 4m - 3 > 0
⇔ m > 3/4
Theo Viét ta có:
x₁ + x₂ = 2m + 1
x₁x₂ = m² + 1
Ta có:
(x₁ + 1)² + (x₂ + 1)² = 13
⇔ x₁² + 2x₁ + 1 + x₂² + 2x₂ + 1 = 13
⇔ (x₁ + x₂)² - 2x₁x₂ + 2(x₁ + x₂) + 2 = 13
⇔ (2m + 1)² - 2(m² + 1) + 2(2m + 1) + 2 = 13
⇔ 4m² + 4m + 1 - 2m² - 2 + 4m + 2 + 2 - 13 = 0
⇔ 2m² + 8m - 10 = 0
Phương trình có hai nghiệm:
m = 1 (nhận)
m = -5 (loại)
Vậy m = 1 thì phương trình có hai nghiệm thỏa mãn (x₁ + 1)² + (x₂ + 1)² = 13
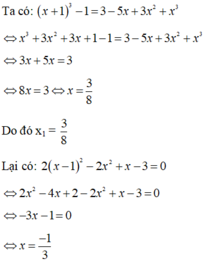
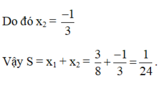
hiệu 2 nghiệm : x1 - x2
=> bình phương hiệu 2 nghiệm: (x1 - x2)2 =13