cho hình vuông ABCD có cạnh bằng a. Trên BC là M, trên tia đối của tia DC lấy N sao cho BM=DN. Vẽ AH vuông góc với NM (H thuộc NM), AH cắt DC tại E. Gọi G là giao điểm của MN với AD. a. Chứng minh tam giác NAM vuông cân và D,H,B thẳng hàng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 12 2018
tam giác NAM chỉ có thể cân thôi ko vuông cân dc,D,H,B đâu có thẳng hàng đâu ta
D
24 tháng 1 2017
Mình sẽ giải ý đầu của câu a à mà bạn tự vẽ hình nha
ý đầu :
Xét \(\Delta\) ABM và \(\Delta\) ADN có:
BM = DN (gt)
góc ABC = góc ADN = 90 độ ( góc ADN kề bù với góc ADE ( E\(\in\)DC)
AB = AD ( ABCD là hình vuông)
=> \(\Delta\) ABM = \(\Delta\) ADN ( c-g-c)
=> AM = AN ( hai cạnh tương ứng )
=> \(\Delta\) NAM cân tại A
Xét \(\Delta\) ANH và \(\Delta\) AMH có:
AM = AN (cmt)
AH cạnh chung
góc AHN = góc AHM = 90 độ
=> \(\Delta\) AHN = \(\Delta\)AHM ( cạnh huyền - cạnh góc vuông)
=> HN = HM ( hai cạnh tương ứng )
Xét \(\Delta\) cân NAM có:
AH vừa là đường cao vừa là đường trung tuyến
=> \(\Delta\) NAM vuông cân tại A.
KV
24 tháng 10 2023
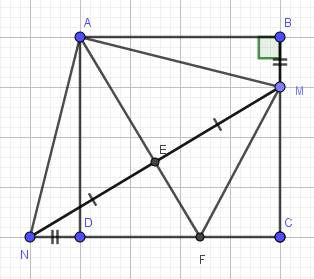
a) Do ABCD là hình vuông (gt)
\(\Rightarrow AB=AD\)
\(\widehat{ABM}=\widehat{ADN}=90^0\)
Xét hai tam giác vuông: \(\Delta ABM\) và \(\Delta ADN\) có:
\(AB=AD\left(cmt\right)\)
\(BM=DN\left(gt\right)\)
\(\Rightarrow\Delta ABM=\Delta ADN\) (hai cạnh góc vuông)
\(\Rightarrow AM=AN\) (hai cạnh tương ứng)
\(\widehat{BAM}=\widehat{DAN}\) (hai góc tương ứng)
Ta có:
\(\widehat{BAM}+\widehat{DAM}=90^0\)
\(\Rightarrow\widehat{DAN}+\widehat{DAM}=90^0\)
\(\Rightarrow\widehat{MAN}=90^0\)
\(\Delta AMN\) có:
\(AM=AN\left(cmt\right)\)
\(\Rightarrow\Delta AMN\) cân tại A
Mà \(\widehat{MAN}=90^0\left(cmt\right)\)
\(\Rightarrow\Delta AMN\) vuông cân tại A
b) Do \(\Delta AMN\) cân tại A
E là trung điểm của MN
\(\Rightarrow AE\) là đường trung tuyến, cũng là đường cao của \(\Delta AMN\)
\(\Rightarrow AE\perp MN\)
\(\Rightarrow EF\perp MN\)
Xét hai tam giác vuông: \(\Delta FEM\) và \(\Delta FEN\) có:
\(EM=EN\left(gt\right)\)
\(EF\) là cạnh chung
\(\Rightarrow\Delta FEM=\Delta FEN\) (hai cạnh góc vuông)
\(\Rightarrow FM=FN\) (hai cạnh tương ứng)
Xét \(\Delta FAN\) và \(\Delta FAM\) có:
\(FA\) là cạnh chung
\(FN=FM\left(cmt\right)\)
\(AN=AM\left(cmt\right)\)
\(\Rightarrow\Delta FAN=\Delta FAM\left(c-c-c\right)\)
