Giải giúp mk bài này nha!^^ Xin cảm ơn nhìu!
Cho hình chữ nhật ABCD. Gọi E là hình chiếu của A trên BD.
a, Chứng minh tam giác AED đồng dạng với tam giác DCB.
b, Chứng minh AD^2=DE.DB
c, Trên DE lấy điểm M, trên BC lấy điểm N sao cho DM/DE = CN/CB. Chứng minh góc DAM = góc CAN.


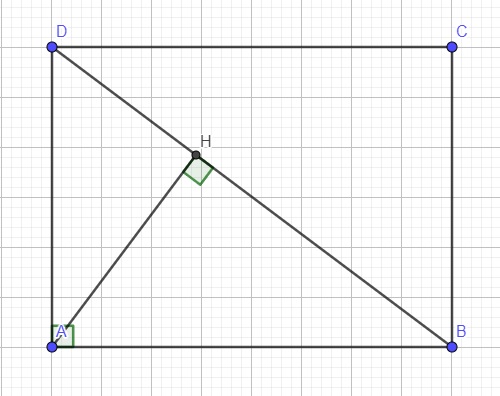
a) Do ABCD là hình chữ nhật \(\Rightarrow AD//BC\)
\(\Rightarrow\widehat{CBD}=\widehat{ADB}\) ( so le trong )
Xét tam giác AED và tam giác DCB có :
\(\widehat{CBD}=\widehat{ADB}\)
\(\widehat{AED}=\widehat{BCD}\left(=90^o\right)\)
\(\Rightarrow\) tam giác AED đồng dạng với tam giác DCB ( g - g ) ( đpcm )
b) \(\Rightarrow\frac{AD}{DB}=\frac{ED}{BC}\)
Mà AD = BC ( do ABCD là hình chữ nhật )
\(\Rightarrow\frac{AD}{DB}=\frac{DE}{AD}\)
\(\Leftrightarrow AD^2=DE\times DB\) ( đpcm )