-3x2 + 14x — 8 = 0
X2 - x - 30 =02
x2 + 3x - 9=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
4
NH
3
A
17 tháng 7 2019
ý bạn là như thế này đúng không ạ:
a/ \(x^2-6x+5=0\)
\(x^2-5x-x+5=0\)
\(x\left(x-5\right)-\left(x-5\right)=0\)
\(\left(x-5\right)\left(x-1\right)=0\)
\(\orbr{\begin{cases}x-5=0\rightarrow x=5\\x-1=0\rightarrow x=1\end{cases}}\)
b/\(2x^2+7x+9=0\)
?!
c/ \(4x^2-7x+3=0\)
\(4x^2-4x-3x+3=0\)
\(4x\left(x-1\right)-3\left(x-1\right)=0\)
\(\left(x-1\right)\left(4x-3\right)=0\)
\(\orbr{\begin{cases}x-1=0\Rightarrow x=1\\4x-3=0\Rightarrow x=\frac{3}{4}\end{cases}}\)
d/ \(2\left(x+5\right)=2x+10\)
-,- mik ko rõ đề ạ, sai thì ibox ạ.Cảm ơn
26 tháng 11 2021
\(x^2=1\Rightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
\(x^2=3\Rightarrow\left[{}\begin{matrix}x=-\sqrt{3}\\x=\sqrt{3}\end{matrix}\right.\)
\(x^2=5\Rightarrow\left[{}\begin{matrix}x=-\sqrt{5}\\x=\sqrt{5}\end{matrix}\right.\Rightarrow x=-\sqrt{5}\left(vì.x< 0\right)\)
\(x^2=7\Rightarrow\left[{}\begin{matrix}x=-\sqrt{7}\\x=\sqrt{7}\end{matrix}\right.\Rightarrow x=-\sqrt{7}\left(vì.x< 0\right)\)
\(x^2=9\Rightarrow\left[{}\begin{matrix}x=-3\\x=3\end{matrix}\right.\)
\(\left(x-2\right)^2=2\Rightarrow\left[{}\begin{matrix}x-2=-\sqrt{2}\\x-2=\sqrt{2}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=2-\sqrt{2}\\x=2+\sqrt{2}\end{matrix}\right.\)
\(\left(x-4\right)^2=4\Rightarrow\left[{}\begin{matrix}x-2=-2\\x-2=2\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
\(\left(x-6\right)^2=6\Rightarrow\left[{}\begin{matrix}x-6=-\sqrt{6}\\x-6=\sqrt{6}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=6-\sqrt{6}\\x=6+\sqrt{6}\end{matrix}\right.\)
\(\left(x-8\right)^2=8\Rightarrow\left[{}\begin{matrix}x-8=-2\sqrt{2}\\x-8=2\sqrt{2}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=8-2\sqrt{2}\\x=2+2\sqrt{2}\end{matrix}\right.\)
\(\left(x-10\right)^2=10\Rightarrow\left[{}\begin{matrix}x-10=-\sqrt{10}\\x-10=\sqrt{10}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=10-\sqrt{10}\\x=10+\sqrt{10}\end{matrix}\right.\)
\(\left(x-\sqrt{3}\right)^2=3\Rightarrow\left[{}\begin{matrix}x-\sqrt{3}=-\sqrt{3}\\x-\sqrt{3}=\sqrt{3}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=2\sqrt{3}\end{matrix}\right.\)
\(\left(x-\sqrt{5}\right)^2=5\Rightarrow\left[{}\begin{matrix}x-\sqrt{5}=-\sqrt{5}\\x-\sqrt{5}=\sqrt{5}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=2\sqrt{5}\end{matrix}\right.\)
J
18 tháng 4 2019
a) \(3x^2-5x+2=0\)
Vì \(a+b+c=3-5+2=0\)
\(\Rightarrow\) pt co 2 ngiệm pb : \(x_1=1\) ; \(x_2=\frac{2}{3}\)
Vậy \(S=\left\{1;\frac{2}{3}\right\}\)
b) \(-3x^2+14x-8=0\)
\(\Delta'=7^2-\left(-3\right)\times\left(-8\right)=49-24=25\)
\(\Rightarrow\) pt có 2 nghiệm pb : \(x_1=4\) ; \(x_2=\frac{2}{3}\)
Vậy \(S=\left\{4;\frac{2}{3}\right\}\)
OP
29 tháng 1 2022
1.
<=> \(\left[{}\begin{matrix}4-3x=0\\10-5x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{4}{3}\\x=2\end{matrix}\right.\)
2.
<=>\(\left[{}\begin{matrix}7-2x=0\\4+8x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=-\dfrac{1}{2}\end{matrix}\right.\)
3.
<=>\(\left[{}\begin{matrix}9-7x=0\\11-3x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{9}{7}\\x=\dfrac{11}{3}\end{matrix}\right.\)
4.
<=>\(\left[{}\begin{matrix}7-14x=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=2\end{matrix}\right.\)
5.
<=>\(\left[{}\begin{matrix}\dfrac{7}{8}-2x=0\\3x+\dfrac{1}{3}=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{16}\\x=-\dfrac{1}{9}\end{matrix}\right.\)
6,7. ko đủ điều kiện tìm
CM
16 tháng 3 2018
a) 8( 3x - 2 ) - 14x = 2( 4 – 7x ) + 15x
⇔ 24x – 16 -14x = 8 – 14x + 15x
⇔ 10x -16 = 8 + x
⇔ 9x = 24
⇔ x = 24/9
b) ( 3x – 1 )( x – 3 ) – 9 + x2 = 0
⇔ (3x -1)( x – 3) + (x - 3)( x + 3) = 0
⇔ (x - 3)(3x - 1 + x - 3) = 0
⇔ (x - 3)(4x - 4) = 0
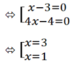
c) |x - 2| = 2x - 3
TH1: x - 2 ≥ 0 ⇔ x ≥ 2
Khi đó: x - 2 = 2x – 3
⇔ 2x – x = -2 + 3
⇔ x = 1 (không TM điều kiện x ≥ 2)
TH2: x – 2 < 0 ⇔ x < 2
Khi đó: x-2 = -(2x – 3)
⇔ x – 2 = -2x + 3
⇔ 3x = 5
⇔ x = 5/3 ( TM điều kiện x < 2)
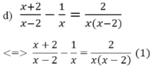
MTC: x(x-2)
ĐKXĐ: x ≠ 0;x ≠ 2
Đối chiếu với ĐKXĐ thì pt có nghiệm x = - 1
Ta có : -3x2 + 14x - 8 = 0
<=> -3x2 + 12x + 2x - 8 = 0
<=> -3x(x - 4) + 2(x - 4) = 0
<=> (x - 4)(2 + 3x) = 0
<=> \(\orbr{\begin{cases}x-4=0\\2+3x=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=4\\3x=-2\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=4\\x=-\frac{2}{3}\end{cases}}\)