tìm giá trị nguyên của x để A \(⋮\)B biết:
\(A=10x^2-7x-5\)và\(B=2x-3\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

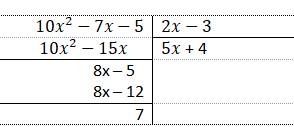
Để \(A⋮B\) thì \(7⋮\left(2x-3\right)\)
\(\Rightarrow2x-3\inƯ\left(7\right)=\left\{-7;-1;1;7\right\}\)
\(\Rightarrow2x\in\left\{-4;2;4;10\right\}\)
\(\Rightarrow x\in\left\{-2;1;2;5\right\}\)

a) ĐKXĐ: \(x\notin\left\{3;-3;-2\right\}\)
Ta có: \(P=\left(\dfrac{2x-1}{x+3}-\dfrac{x}{3-x}-\dfrac{3-10x}{x^2-9}\right):\dfrac{x+2}{x-3}\)
\(=\left(\dfrac{\left(2x-1\right)\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}+\dfrac{x\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}-\dfrac{3-10x}{\left(x-3\right)\left(x+3\right)}\right):\dfrac{x+2}{x-3}\)
\(=\dfrac{2x^2-6x-x+3+x^2+3x-3+10x}{\left(x-3\right)\left(x+3\right)}:\dfrac{x+2}{x-3}\)
\(=\dfrac{3x^2+6x}{\left(x-3\right)\left(x+3\right)}:\dfrac{x+2}{x-3}\)
\(=\dfrac{3x\left(x+2\right)}{\left(x-3\right)\left(x+3\right)}\cdot\dfrac{x-3}{x+2}\)
\(=\dfrac{3x}{x+3}\)
b) Ta có: \(x^2-7x+12=0\)
\(\Leftrightarrow x^2-3x-4x+12=0\)
\(\Leftrightarrow x\left(x-3\right)-4\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\left(loại\right)\\x=4\left(nhận\right)\end{matrix}\right.\)
Thay x=4 vào biểu thức \(P=\dfrac{3x}{x+3}\), ta được:
\(P=\dfrac{3\cdot4}{4+3}=\dfrac{12}{7}\)
Vậy: Khi \(x^2-7x+12=0\) thì \(P=\dfrac{12}{7}\)

\(a,P=\left(\dfrac{2x-1}{x+3}-\dfrac{x}{3-x}-\dfrac{3-10x}{x^2-9}\right):\dfrac{x+2}{x-3}\left(x\ne\pm3;x\ne-2\right)\\ P=\dfrac{2x^2-7x+3+x^2+3x-3+10x}{\left(x-3\right)\left(x+3\right)}\cdot\dfrac{x-3}{x+2}\\ P=\dfrac{3x^2+6x}{\left(x-3\right)\left(x+2\right)}=\dfrac{3x\left(x+2\right)}{\left(x-3\right)\left(x+2\right)}=\dfrac{3x}{x-3}\\ b,x^2-7x+12=0\\ \Leftrightarrow\left(x-3\right)\left(x-4\right)=0\\ \Leftrightarrow x=4\left(x\ne3\right)\\ \Leftrightarrow A=\dfrac{3\cdot4}{4-3}=12\\ c,P=\dfrac{3\left(x-3\right)+9}{x-3}=3+\dfrac{9}{x-3}\in Z\\ \Leftrightarrow x-3\inƯ\left(9\right)=\left\{-9;-3;-1;1;3;9\right\}\\ \Leftrightarrow x\in\left\{-6;0;2;4;6;12\right\}\)

a) f(x) = 10x² - 7x - 5 = 10x² - 15x + 8x - 12 + 7 = 5x(2x-3) + 4(2x-3) + 7
f(x) chia hết cho 2x-3 khi và chỉ khi 7 chia hết cho 2x-3, vì 7 là số nguyên tố, nên chi có các trường hợp:
TH1: 2x-3 = -1 <=> x = 1
TH2: 2x-3 = 1 <=> x = 2
TH3: 2x-3 = -7 <=> x = -2
TH4: 2x-3 = 7 <=> x = 5
Vây có 4 giá trị nguyên của x là {-2, 1, 2, 5}
a) f(x) = 10x² - 7x - 5 = 10x² - 15x + 8x - 12 + 7 = 5x(2x-3) + 4(2x-3) + 7
f(x) chia hết cho 2x-3 khi và chỉ khi 7 chia hết cho 2x-3, vì 7 là số nguyên tố, nên chi có các trường hợp:
TH1: 2x-3 = -1 <=> x = 1
TH2: 2x-3 = 1 <=> x = 2
TH3: 2x-3 = -7 <=> x = -2
TH4: 2x-3 = 7 <=> x = 5
Vây có 4 giá trị nguyên của x là {-2, 1, 2, 5}
b) g(x) = x³ - 4x² + 5x - 1 = x³ - 3x² - x² + 3x + 2x - 6 + 5 = x²(x-3) - x(x-3) + 2(x-3) + 5
g(x) chia hết cho x-3 khi và chỉ khi 5 chia hết cho x-3 (5 là số nguyên tố nên chỉ xét các trường hợp)
TH1: x-3 = -5 <=> x = -2
TH2: x-3 = -1 <=> x = 2
TH3: x-3 = 1 <=> x = 4
TH4: x-3 = 5 <=> x = 8
Vậy có giá trị nguyên của x thỏa là {-1, 2, 4, 8}

a) \(x^3-5x^2+8x-4=\left(x^3-x^2\right)-4\left(x^2-x\right)+4\left(x-1\right)=x^2\left(x-1\right)-4x\left(x-1\right)+4\left(x-1\right)\)
\(=\left(x-1\right)\left(x^2-4x+4\right)=\left(x-1\right)\left(x-2\right)^2\)
b) \(A=5x\left(2x-3\right)+4\left(2x-3\right)+7\) chia hết cho 2x-3 => 7 chia hết cho 2x -3
=> 2x -3 thuộc U(7) ={-7;-1;1;7}
+2x-3 =-7 => x =-2
+2x-3 =-1 => x =1
+2x-3 =1 => x =2
+2x -3 =7 => x =5

Để \(A⋮B\) thì \(10x^2-7x-5⋮2x-3\)
\(\Leftrightarrow10x^2-15x+8x-12+7⋮2x-3\)
\(\Leftrightarrow5x\left(2x-3\right)+4\left(2x-3\right)+7⋮2x-3\)
\(\Leftrightarrow\left(2x-3\right)\left(5x+4\right)+7⋮2x-3\)
mà \(\left(2x-3\right)\left(5x+4\right)⋮2x-3\)
nên \(7⋮2x-3\)
\(\Leftrightarrow2x-3\inƯ\left(7\right)\)
\(\Leftrightarrow2x-3\in\left\{1;-1;7;-7\right\}\)
\(\Leftrightarrow2x\in\left\{4;2;10;-4\right\}\)
hay \(x\in\left\{2;1;5;-2\right\}\)(nhận)
Vậy: Khi \(x\in\left\{2;1;5;-2\right\}\) thì \(A⋮B\)
Điều kiện: \(B\ne0\Leftrightarrow2x-3\ne0\Leftrightarrow x\ne\dfrac{3}{2}\).
Ta có: \(\dfrac{A}{B}=\dfrac{10x^2-7x-5}{2x-3}=\dfrac{10x^2-15x+8x-12+7}{2x-3}\\ =\dfrac{5x\left(2x-3\right)+4\left(2x-3\right)+7}{2x-3}=5x+4+\dfrac{7}{2x-3}\)
Để \(A⋮B\) thì \(\left(2x-3\right)\inƯ\left(7\right)=\left\{\pm1;\pm7\right\}\)
Nếu \(2x-3=1\Leftrightarrow2x=4\Leftrightarrow x=2\) (Thỏa mãn)
Nếu \(2x-3=-1\Leftrightarrow2x=2\Leftrightarrow x=1\) (Thỏa mãn)
Nếu \(2x-3=7\Leftrightarrow2x=10\Leftrightarrow x=5\) (Thỏa mãn)
Nếu \(2x-3=-7\Leftrightarrow2x=-4\Leftrightarrow x=-2\) (Thỏa mãn).
Vậy tập các giá trị \(x\) thỏa mãn là \(\left\{1;\pm2;5\right\}\).

`M=(10x^2-7x-5)/(2x-3)(x ne 3/2)`
`=(10x^2-15x+8x-12+7)/(2x-3)`
`=(5x(2x-3)+4(2x-3)+7)/(2x-3)`
`=5x+4+7/(2x-3)`
Để `M in ZZ`
`=>7/(2x-3) in ZZ`
`=>2x-3 in Ư(7)={+-1,+-7}`
`=>2x in {2,4,-4,10}`
`=>x in {1,2,-2,5}(tm)`
Vậy `x in {1,2,-2,5}` thì `M in ZZ`.
x = 2;5/2;11;41/2
\(A=10x^2-7x-5=\left(10x^2-15x\right)+8x-12+7=5x\left(2x-3\right)+4\left(2x-3\right)+7\)
\(A⋮B\Leftrightarrow7⋮2x+3\)
Rồi xét từng ước và tìm x