K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
M
giải hộ mình mấy bài này vs ạ !
2
6 tháng 5 2021
Bài 5 hình 1: (tự vẽ hình nhé bạn)
a) Xét ΔABD và ΔACB ta có:
\(\widehat{BAD}\)= \(\widehat{BAC}\) (góc chung)
\(\widehat{ABD}\)= \(\widehat{ACB}\) (gt)
=> ΔABD ~ ΔACB (g-g)
=> \(\dfrac{AB}{AC}\) = \(\dfrac{BD}{CB}\) = \(\dfrac{AD}{AB}\) (tsđd)
b) Ta có: \(\dfrac{AB}{AC}\) = \(\dfrac{AD}{AB}\) (cm a)
=> \(AB^2\) = AD.AC
=> \(2^2\) = AD.4
=> AD = 1 (cm)
Ta có: AC = AD + DC (D thuộc AC)
=> 4 = 1 + DC
=> DC = 3 (cm)
c) Xét ΔABH và ΔADE ta có:
\(\widehat{AHB}\) = \(\widehat{AED}\) (=\(90^0\))
\(\widehat{ADB}\) = \(\widehat{ABH}\) (ΔABD ~ ΔACB)
=> ΔABH ~ ΔADE
=> \(\dfrac{AB}{AD}\) = \(\dfrac{AH}{AE}\) = \(\dfrac{BH}{DE}\) (tsdd)
Ta có: \(\dfrac{S_{ABH}}{S_{ADE}}\) = \(\left(\dfrac{AB}{AD}\right)^2\)= \(\left(\dfrac{2}{1}\right)^2\)= 4
=> đpcm
6 tháng 5 2021
Tiếp bài 5 hình 2 (tự vẽ hình)
a) Xét ΔABC vuông tại A ta có:
\(BC^2\) = \(AB^2\) + \(AC^2\)
\(BC^2\) = \(21^2\) + \(28^2\)
BC = 35 (cm)
b) Xét ΔABC và ΔHBA ta có:
\(\widehat{BAC}\) = \(\widehat{AHB}\) ( =\(90^0\))
\(\widehat{ABC}\) = \(\widehat{ABH}\) (góc chung)
=> ΔABC ~ ΔHBA (g-g)
=> \(\dfrac{AB}{BH}\) = \(\dfrac{BC}{AB}\) (tsdd)
=> \(AB^2\) = BH.BC
=> \(21^2\) = 35.BH
=> BH = 12,6 (cm)
c) Xét ΔABC ta có:
BD là đường p/g (gt)
=> \(\dfrac{AD}{DC}\) = \(\dfrac{AB}{BC}\) (t/c đường p/g)
Xét ΔABH ta có:
BE là đường p/g (gt)
=> \(\dfrac{HE}{AE}\) = \(\dfrac{BH}{AB}\) (t/c đường p/g)
Mà: \(\dfrac{AB}{BC}\) = \(\dfrac{BH}{AB}\) (cm b)
=> đpcm
d) Ta có: \(\left\{{}\begin{matrix}\widehat{HBE}+\widehat{BEH}=90^0\\\widehat{ABD}+\widehat{ADB=90^0}\\\widehat{HBE}=\widehat{ABD}\end{matrix}\right.\)
=> \(\widehat{BEH}=\widehat{ADB}\)
Mà \(\widehat{BEH}=\widehat{AED}\) (2 góc dd)
Nên \(\widehat{ADB}=\widehat{AED}\)
=> đpcm
TK
1
NT
14 tháng 4 2021
a,Nd:tuyên bố kết quả ,khẳng định sự nghiệp chính nghĩa
NX: bằng việc sd BP liệt kê ,chứng cứ xác thực 7 câu thơ cuối chính là lời khẳng định đanh thép về sức mạnh của chân lí ,chính nghĩa là lẽ phải ko có gì chối cãi được
DT
Đỗ Thanh Hải
CTVVIP
6 tháng 7 2021
1 because
2 as long as
3 although
4 so that
5 although
6 even if
7 until
8 while
9 because
10 Although
DT
Đỗ Thanh Hải
CTVVIP
20 tháng 5 2021
1 A
2 D
3 B
4 C
5 C
II
1 B
2 C
3 C
4 A
5 C
III
1 - B
2 - C
3 - A
4 - E
5 - F
B
6 so
7 or
8 because
9 and
10 more
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 7 2021
\(M=\left(\dfrac{\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\right).\dfrac{\sqrt{x}-2}{2}\)
\(=\dfrac{2\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{2\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\)
2. Ta có:
\(\sqrt{x}>0\Rightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}+2}>0\) hay \(M>0\)
Lại có: \(M=\dfrac{\sqrt{x}+2-1}{\sqrt{x}+2}=1-\dfrac{1}{\sqrt{x}+2}< 1\)
\(\Rightarrow0< M< 1\Rightarrow M>M^2\)
10 tháng 7 2021
1) Ta có: \(M=\left(\dfrac{\sqrt{x}}{x-4}+\dfrac{1}{\sqrt{x}-2}\right)\cdot\dfrac{\sqrt{x}-2}{2}\)
\(=\dfrac{\sqrt{x}+\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}-2}{2}\)
\(=\dfrac{2\sqrt{x}+2}{2\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\)
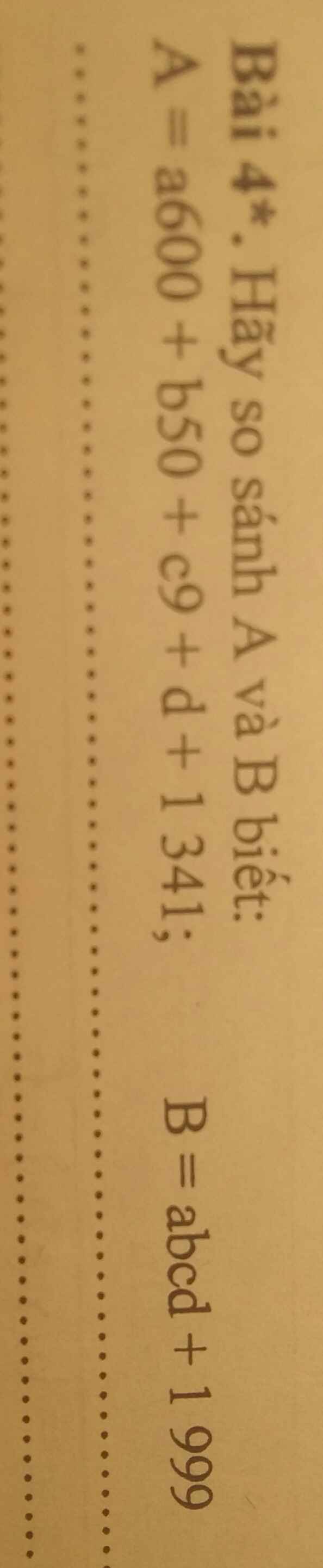
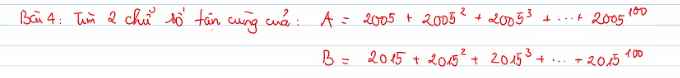
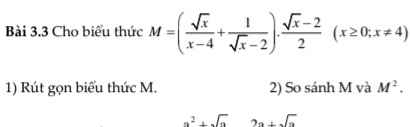
mo lam
sự vật: chúng
hoạt động : gọi,trò chuyện, trêu ghẹo, tranh cãi nhau, tuởng tuợng
đặc điểm:ồn ào ,vui , ko thể