Tìm tổng tất cả các giá trị thực của tham số
m sao cho đường thẳng đi qua hai điểm cực trị của đồ thị hàm số
\(y=2x^3+3\left(m-1\right)x^2+6m\left(1-2m\right)x.\) song song đường thẳng y= -4x
.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : \(y'=3x^2+3m\)
Điều kiện để hàm số có 2 điểm cực trị là y'=0 có 2 nghiệm phân biệt
\(\Leftrightarrow 3x^2=-3m\) có 2 nghiệm phân biệt
\(\Leftrightarrow m<0\)
Đường thẳng đi qua 2 điểm cực trị là phần dư khi lấy y chia cho y':
\(x^3+3mx+1=\dfrac{x}{3}.(3x^2+3m)+2mx+1\)
\(=>\) đường thẳng đi qua 2 điểm cực trị có dạng: \(y=2mx+1\)
\(\Leftrightarrow 2mx-y+1=0\) \((\Delta)\)
\(d_{(M,\Delta)}=\dfrac{|0.2m+3.(-1)+1|}{\sqrt{4m^2+1}}=\dfrac{2}{\sqrt{5}}\)
\(\Leftrightarrow 4m^2+1=5 \Leftrightarrow m^2=1 \Leftrightarrow m=\pm1\)
Đối chiếu với điều kiện ta được \(m=1\)

a: Thay x=2 và y=-3 vào (d), ta được:
\(2\left(2m-1\right)-2m+5=-3\)
=>\(4m-2-2m+5=-3\)
=>2m+3=-3
=>2m=-6
=>\(m=-\dfrac{6}{2}=-3\)
b: Để (d)//(d') thì \(\left\{{}\begin{matrix}2m-1=2\\-2m+5\ne1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2m=3\\-2m\ne-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{3}{2}\\m\ne2\end{matrix}\right.\)
=>m=3/2
Thay m=3/2 vào (d), ta được:
\(y=\left(2\cdot\dfrac{3}{2}-1\right)x-2\cdot\dfrac{3}{2}+5=2x+2\)

y=2x+2 nên a=2
Gọi \(\alpha\) là góc tạo bởi (d) với trục Ox
\(tan\alpha=2\)
=>\(\alpha\simeq63^026'\)

a) Để đồ thị hàm số \(y=\left(m-2\right)x+2\) đồng biến trên R.
=> \(m-2>0.\)
<=> \(m>2.\)
b) Đồ thị hàm số \(y=\left(m-2\right)x+2\) song song với đường thẳng \(y=5x+1.\)
=> \(m-2=5.\)
<=> \(m=7.\)
Câu 2
a) Để hs đã cho đồng biến trên R thì:
\(m-2>0\\ < =>m>2\)
b) Đề đths đã cho song song với đường thẳng \(y=5x+1\) thì:
\(m-2=5\\ < =>m=7\)

Chọn C
[Phương pháp tự luận]
Ta có : y = 6 x 2 - 6 ( m + 1 ) x + 6 m
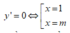
Điều kiện để hàm số có 2 điểm cực trị là m ≠ 1
![]()
Hệ số góc đt AB là k = - ( m - 1 ) 2
Đt AB vuông góc với đường thẳng y = x + 2
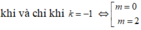

+ Ta có đạo hàm y’ = 6x2- 6( m+ 1) x+ 6m
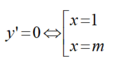
Điều kiện để hàm số có 2 điểm cực trị là : m≠ 1
Tọa độ 2 điểm cực trị là A( 1 ; 3m-1) và B ( m ; -m3+ 3m2)
+ Hệ số góc đường thẳng AB là :k= - ( m-1) 2
+ Đường thẳng AB vuông góc với đường thẳng y= x+ 2 khi và chỉ khi k= -1
Hay – ( m-1) 2= -1( vì 2 đường thẳng vuông góc với nhau thì tích hai hệ số góc bằng -1) 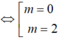
Chọn C.

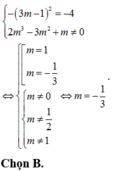


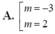

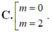
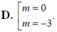
Chứng minh công thức tổng quát phương trình đi qua 2 điểm cực trị:
giả sử hàm bậc 3: \(y=ax^3+bxx^2+cx+d\left(a\ne0\right)\) có 2 điểm cực trị x1;x2
Ta đi tìm số dư 1 cách tổng quát:
Ta có: \(y'=3ax^2+2bx+c-và-y''=6ax+b\)
Xét phép chia giữa y' và y'' ta có: \(y=y'\left(\dfrac{1}{3}x+\dfrac{b}{9a}\right)+g\left(x\right)\left(1\right)\) là phường trình đi qua 2 điểm cực trị của đồ thị hàm số bậc 3
từ (1) Ta có: \(y=y'\dfrac{3ax+b}{9a}+g\left(x\right)-hay-y=y'\dfrac{6ax+2b}{18a}g\left(x\right)\)
Từ đây dễ suy ra: \(g\left(x\right)=y-\dfrac{y'.y''}{18a}\left(công-thức-tổng-quát\right)\) ( dĩ nhiên bạn chỉ cần nhớ cái này )
áp dụng vào bài toán ta có:
\(2x^3+3\left(m-1\right)x^2+6m\left(1-2m\right)x-\left(6x^2+6\left(m-1\right)x+6m\left(1-2m\right)\right).\dfrac{12x+6\left(m-1\right)}{18.2}\)
Gán: \(\left\{{}\begin{matrix}x=i\\m=10\end{matrix}\right.\) => 1710-841i
\(\Rightarrow y=4m\left(-2m-1\right)x+17m^2+m\) bài toán quay trở về bài toán đơn giản bạn giải nốt là oke
Khiếp học ghê như vầy bảo dạy người ta thì kêu thôi, sợ sót kiến thức :)))?