Bài 1 (2đ): Giải phương trình và hệ phương trình sau:
a)3x2 – 26x + 49 = 0
b)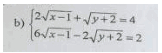 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 2 2021
a. (3x - 1)2 - (x + 3)2 = 0
\(\Leftrightarrow\left(3x-1+x+3\right)\left(3x-1-x-3\right)=0\)
\(\Leftrightarrow\left(4x+2\right)\left(2x-4\right)=0\)
\(\Leftrightarrow4x+2=0\) hoặc \(2x-4=0\)
1. \(4x+2=0\Leftrightarrow4x=-2\Leftrightarrow x=-\dfrac{1}{2}\)
2. \(2x-4=0\Leftrightarrow2x=4\Leftrightarrow x=2\)
S=\(\left\{-\dfrac{1}{2};2\right\}\)
28 tháng 2 2021
b. \(x^3=\dfrac{x}{49}\)
\(\Leftrightarrow49x^3=x\)
\(\Leftrightarrow49x^3-x=0\)
\(\Leftrightarrow x\left(49x^2-1\right)=0\)
\(\Leftrightarrow x\left(7x+1\right)\left(7x-1\right)=0\)
\(\Leftrightarrow x=0\) hoặc \(7x+1=0\) hoặc \(7x-1=0\)
1. x=0
2. \(7x+1=0\Leftrightarrow7x=-1\Leftrightarrow x=-\dfrac{1}{7}\)
3. \(7x-1=0\Leftrightarrow7x=1\Leftrightarrow x=\dfrac{1}{7}\)
28 tháng 6 2023
3:
a: u+v=14 và uv=40
=>u,v là nghiệm của pt là x^2-14x+40=0
=>x=4 hoặc x=10
=>(u,v)=(4;10) hoặc (u,v)=(10;4)
b: u+v=-7 và uv=12
=>u,v là các nghiệm của pt:
x^2+7x+12=0
=>x=-3 hoặc x=-4
=>(u,v)=(-3;-4) hoặc (u,v)=(-4;-3)
c; u+v=-5 và uv=-24
=>u,v là các nghiệm của phương trình:
x^2+5x-24=0
=>x=-8 hoặc x=3
=>(u,v)=(-8;3) hoặc (u,v)=(3;-8)
3 tháng 3 2022
\(a,3x^2+5x+2=0\\ \Leftrightarrow\left(3x^2+3x\right)+\left(2x+2\right)=0\\ \Leftrightarrow3x\left(x+1\right)+2\left(x+1\right)=0\\ \Leftrightarrow\left(3x+2\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{2}{3}\\x=-1\end{matrix}\right.\)
b, ĐKXĐL\(x\ne\pm\dfrac{2}{3}\)
\(\dfrac{3x+2}{3x-2}-\dfrac{6}{2+3x}=\dfrac{9x^2}{9x^2-4}\\ \Leftrightarrow\dfrac{\left(3x+2\right)^2}{\left(3x+2\right)\left(3x-2\right)}-\dfrac{6\left(3x-2\right)}{\left(3x+2\right)\left(3x-2\right)}-\dfrac{9x^2}{\left(3x+2\right)\left(3x-2\right)}=0\\ \Leftrightarrow\dfrac{9x^2+12x+4-18x+12-9x^2}{\left(3x+2\right)\left(3x-2\right)}=0\\ \Leftrightarrow-6x+16=0\\ \Leftrightarrow x=\dfrac{8}{3}\left(tm\right)\)
DT
Đỗ Thanh Hải
CTVVIP
16 tháng 4 2021
1) \(\left\{{}\begin{matrix}2x+y=10\\5x-3y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}10x+5y=50\\10x-6y=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}11y=44\\2x+y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=4\\x=3\end{matrix}\right.\)
Vậy hpt có nghiệm (x;y) = (3;4)
2)
a) 3x2 - 2x - 1 = 0
\(\Leftrightarrow3x^2-3x+x-1=0\)
\(\Leftrightarrow3x\left(x-1\right)+\left(x-1\right)=0\)
\(\Leftrightarrow\left(3x+1\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=1\end{matrix}\right.\)
Vậy pt có nghiệm x = 1 hoặc x = 3
b) Đặt x2 = t (t \(\ge\) 0)
Pt trở thành: t2 - 20t + 4 = 0
\(\Delta\) = (-20)2 - 4.1.4 = 400 - 16 = 384
=> pt có 2 nghiệm phân biệt t1 = \(\dfrac{20+8\sqrt{6}}{2}=10+4\sqrt{6}\)
t2 = \(\dfrac{20-8\sqrt{6}}{2}=10-4\sqrt{6}\)
=> x1 = \(\sqrt{10+4\sqrt{6}}=\sqrt{\left(2+\sqrt{6}\right)^2}=2+\sqrt{6}\)
x2 = \(2-\sqrt{6}\)
AH
Akai Haruma
Giáo viên
12 tháng 5 2021
Lời giải:
a) $|4x^2-25|=0$
$\Leftrightarrow 4x^2-25=0$
$\Leftrightarrow (2x-5)(2x+5)=0$
$\Rightarrow x=\pm \frac{5}{2}$
b)
$|x-2|=3$
\(\Rightarrow \left[\begin{matrix} x-2=-3\\ x-2=3\end{matrix}\right.\Rightarrow \left[\begin{matrix} x=-1\\ x=5\end{matrix}\right.\)
c)
\(|x-3|=2x-1\Rightarrow \left\{\begin{matrix} 2x-1\geq 0\\ \left[\begin{matrix} x-3=2x-1\\ x-3=1-2x\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ \left[\begin{matrix} x=-2\\ x=\frac{4}{3}\end{matrix}\right.\end{matrix}\right.\Rightarrow x=\frac{4}{3}\)
d)
$|x-5|=|3x-2|$
\(\Rightarrow \left[\begin{matrix} x-5=3x-2\\ x-5=2-3x\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=\frac{-3}{2}\\ x=\frac{7}{4}\end{matrix}\right.\)
CM
2 tháng 7 2017
a) 3 x 2 − 7 x − 10 ⋅ 2 x 2 + ( 1 − 5 ) x + 5 − 3 = 0
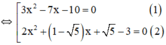
+ Giải (1):
3 x 2 – 7 x – 10 = 0
Có a = 3; b = -7; c = -10
⇒ a – b + c = 0
⇒ (1) có hai nghiệm x 1 = - 1 v à x 2 = - c / a = 10 / 3 .
+ Giải (2):
2 x 2 + ( 1 - √ 5 ) x + √ 5 - 3 = 0
Có a = 2; b = 1 - √5; c = √5 - 3
⇒ a + b + c = 0
⇒ (2) có hai nghiệm:
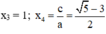
Vậy phương trình có tập nghiệm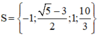 
b)
x 3 + 3 x 2 - 2 x - 6 = 0 ⇔ x 3 + 3 x 2 - ( 2 x + 6 ) = 0 ⇔ x 2 ( x + 3 ) - 2 ( x + 3 ) = 0 ⇔ x 2 - 2 ( x + 3 ) = 0
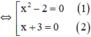
+ Giải (1): x 2 – 2 = 0 ⇔ x 2 = 2 ⇔ x = √2 hoặc x = -√2.
+ Giải (2): x + 3 = 0 ⇔ x = -3.
Vậy phương trình có tập nghiệm S = {-3; -√2; √2}
c)
x 2 − 1 ( 0 , 6 x + 1 ) = 0 , 6 x 2 + x ⇔ x 2 − 1 ( 0 , 6 x + 1 ) = x ⋅ ( 0 , 6 x + 1 ) ⇔ x 2 − 1 ( 0 , 6 x + 1 ) − x ( 0 , 6 x + 1 ) = 0 ⇔ ( 0 , 6 x + 1 ) x 2 − 1 − x = 0
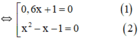
+ Giải (1): 0,6x + 1 = 0 ⇔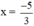 
+ Giải (2):
x 2 – x – 1 = 0
Có a = 1; b = -1; c = -1
⇒ Δ = ( - 1 ) 2 – 4 . 1 . ( - 1 ) = 5 > 0
⇒ (2) có hai nghiệm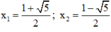 
Vậy phương trình có tập nghiệm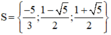 
d)
x 2 + 2 x − 5 2 = x 2 − x + 5 2 ⇔ x 2 + 2 x − 5 2 − x 2 − x + 5 2 = 0 ⇔ x 2 + 2 x − 5 − x 2 − x + 5 ⋅ x 2 + 2 x − 5 + x 2 − x + 5 = 0 ⇔ ( 3 x − 10 ) 2 x 2 + x = 0
⇔ (3x-10).x.(2x+1)=0
+ Giải (1): 3x – 10 = 0 ⇔ 
+ Giải (2):
9 tháng 3 2023
Bài 2:
a: =>2x^2-4x+1=x^2+x+5
=>x^2-5x-4=0
=>\(x=\dfrac{5\pm\sqrt{41}}{2}\)
b: =>11x^2-14x-12=3x^2+4x-7
=>8x^2-18x-5=0
=>x=5/2 hoặc x=-1/4
CM
6 tháng 4 2017
a) x 2 – 4 = 0: đây là phương trình bậc hai; a = 1; b = 0; c = - 4
b) x 3 + 4 x 2 – 2 = 0 : đây không là phương trình bậc hai
c) 2 x 2 + 5 x = 0 : đây là phương trình bậc hai; a = 2; b = 5; c = - 5
d) 4x – 5 = 0 đây không là phương trình bậc hai
e) - 3 x 2 = 0 đây là phương trình bậc hai; a = -3; b = 0; c = 0
\(3x^2-26x+49=0\left(a=3;b^,=-13;c=49\right)\)
\(\Delta^,=\left(-13\right)^2-3.49=22\Rightarrow\sqrt{\Delta^,}=\sqrt{22}\)
Do \(\Delta^,>0\)nên phương trình đã cho có 2 nghiệm phân biệt là
\(x_1=\frac{13-\sqrt{22}}{3};x_2=\frac{13+\sqrt{22}}{3}\)