Tìm nghiệm của đa thức:
C(x)= 1/2 mũ 3-2x
D(x) = 2x mũ 2- 5x-7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 5 2022
a: \(H\left(x\right)=-x^5+x^4-3x^3+2x^2-5x-2+x^5-x^4+3x^3-2x^2+3x+11\)
=-2x+9
Đặt H(x)=0
=>-2x+9=0
hay x=-9/2
b: Vì H(9)<>0 nên x=9 ko là nghiệm của H(x)
NH
13 tháng 4 2023
a: H(x)=−x5+x4−3x3+2x2−5x−2+x5−x4+3x3−2x2+3x+11�(�)=−�5+�4−3�3+2�2−5�−2+�5−�4+3�3−2�2+3�+11
=-2x+9
Đặt H(x)=0
=>-2x+9=0
hay x=-9/2
b: Vì H(9)<>0 nên x=9 ko là nghiệm của H(x)
14 tháng 7 2023
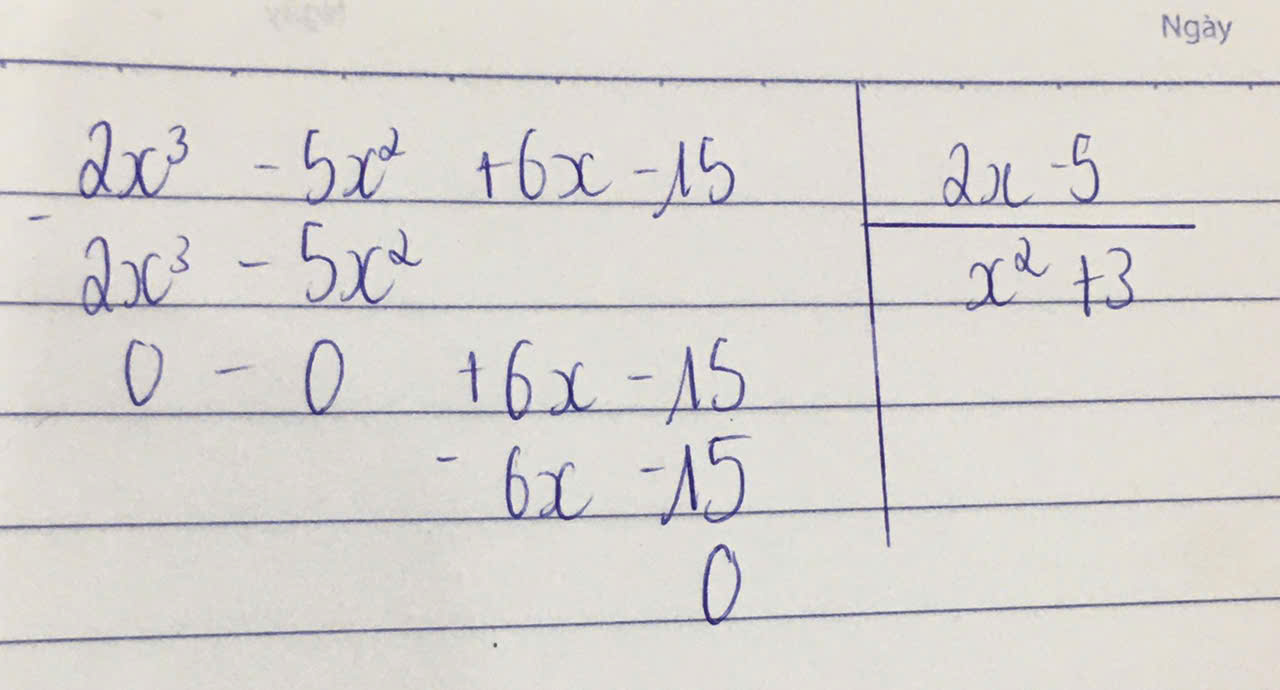
1: x^2-9x+8=0
=>(x-1)(x-8)=0
=>x=1 hoặc x=8
2: 3x^2-7x+4=0
=>3x^2-3x-4x+4=0
=>(x-1)(3x-4)=0
=>x=4/3 hoặc x=1
3: 2x^2+5x-7=0
=>(2x+7)(x-1)=0
=>x=1 hoặc x=-7/2
4: 3x^2-9x+6=0
=>x^2-3x+2=0
=>x=1 hoặc x=2
5: x^2+2x-3=0
=>(x+3)(x-1)=0
=>x=-3 hoặc x=1
NN
14 tháng 7 2023
`@` `\text {Answer}`
`\downarrow`
`1)`
\(x^2 - 9x + 8?\)
\(x^2-9x+8=0\)
`<=>`\(x^2-8x-x+8=0\)
`<=> (x^2 - 8x) - (x - 8) = 0`
`<=> x(x - 8) - (x-8) = 0`
`<=> (x-1)(x-8) = 0`
`<=>`\(\left[{}\begin{matrix}x-1=0\\x-8=0\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}x=1\\x=8\end{matrix}\right.\)
Vậy, nghiệm của đa thức là `S = {1; 8}`
`2)`
\(3x^2 - 7x + 4 =0\)
`<=> 3x^2 - 3x - 4x + 4 = 0`
`<=> (3x^2 - 3x) - (4x - 4) = 0`
`<=> 3x(x - 1) - 4(x - 1) = 0`
`<=> (3x - 4)(x-1) = 0`
`<=>`\(\left[{}\begin{matrix}3x-4=0\\x-1=0\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}3x=4\\x=1\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}x=\dfrac{4}{3}\\x=1\end{matrix}\right.\)
Vậy, nghiệm của đa thức là `S = {4/3; 1}`
`3)`
\(2x^2 + 5x - 7=0\)
`<=> 2x^2 - 2x + 7x - 7 = 0`
`<=> (2x^2 - 2x) + (7x - 7) = 0`
`<=> 2x(x - 1) + 7(x - 1) = 0`
`<=> (2x+7)(x-1) = 0`
`<=>`\(\left[{}\begin{matrix}2x+7=0\\x-1=0\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}2x=-7\\x=1\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}x=-\dfrac{7}{2}\\x=1\end{matrix}\right.\)
Vậy, nghiệm của đa thức là `S = {-7/2; 1}.`
Để đa thức \(C\left(x\right),D\left(x\right)\) có nghiệm thì \(C\left(x\right)=0,D\left(x\right)=0\)
Do đó : \(C\left(x\right)=\left(\dfrac{1}{2}\right)^3-2x=0\)
\(\Rightarrow\dfrac{1}{8}-2x=0\)
\(\Rightarrow2x=\dfrac{1}{8}\)
\(\Rightarrow x=\dfrac{1}{8}:2=\dfrac{1}{16}\)
Vậy \(x=\dfrac{1}{16}\) là nghiệm của đa thức \(C\left(x\right)\)
\(D\left(x\right)=2x^2-5x-7=0\)
\(\Rightarrow2x^2+2x-7x-7=0\)
\(\Rightarrow2x\left(x+1\right)-7\left(x+1\right)=0\)
\(\Rightarrow\left(x+1\right)\left(2x-7\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+1=0\\2x-7=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{7}{2}\end{matrix}\right.\)
Vậy \(x\in\left\{-1;\dfrac{7}{2}\right\}\) là nghiệm của đa thức \(D\left(x\right)\)