
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(S=\dfrac{1}{2^2}+\dfrac{1}{\left(2.2\right)^2}+\dfrac{1}{\left(2.3\right)^2}+...+\dfrac{1}{\left(2.10\right)^2}\)
\(=\dfrac{1}{2^2}+\dfrac{1}{2^2.2^2}+\dfrac{1}{2^2.3^2}+...+\dfrac{1}{2^2.10^2}\)
\(=\dfrac{1}{2^2}\left(1+\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{10^2}\right)\)
\(< \dfrac{1}{2^2}\left(1+\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{9.10}\right)\)
\(=\dfrac{1}{4}\left(1+1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{9}-\dfrac{1}{10}\right)\)
\(=\dfrac{1}{4}\left(2-\dfrac{1}{10}\right)< \dfrac{1}{4}.2=\dfrac{1}{2}\) (đpcm)

4b.
\(\dfrac{\pi}{2}< a< \pi\Rightarrow cosa< 0\Rightarrow cosa=-\sqrt{1-sin^2a}=-\dfrac{4}{5}\)
\(\Rightarrow tana=\dfrac{sina}{cosa}=-\dfrac{3}{4}\)
\(tan\left(a+\dfrac{\pi}{3}\right)=\dfrac{tana+tan\left(\dfrac{\pi}{3}\right)}{1-tana.tan\left(\dfrac{\pi}{3}\right)}=\dfrac{-\dfrac{3}{4}+\sqrt{3}}{1-\left(-\dfrac{3}{4}\right).\sqrt{3}}=...\)
c.
\(\dfrac{3\pi}{2}< a< 2\pi\Rightarrow cosa>0\Rightarrow cosa=\sqrt{1-sin^2a}=\dfrac{5}{13}\)
\(cos\left(\dfrac{\pi}{3}-a\right)=cos\left(\dfrac{\pi}{3}\right).cosa+sin\left(\dfrac{\pi}{3}\right).sina=\dfrac{1}{2}.\dfrac{5}{13}+\left(-\dfrac{12}{13}\right).\dfrac{\sqrt{3}}{2}=...\)


\(Cau.23:\\ N=\left(A_1+T_1+G_1+X_1\right).2=\left(100+200=300+400\right).2=2000\left(Nu\right)\\ L=\dfrac{N}{2}.3,4=\dfrac{2000}{2}.3,4=3400\left(A^o\right)\\ Chon.C\)

const fi='kt.txt';
fo='kq.out';
var f1,f2:text;
s:string;
i,dem,d:integer;
begin
assign(f1,fi); reset(f1);
assign(f2,fo); rewrite(f2);
readln(f1,s);
d:=length(s);
dem:=0;
for i:=1 to d do
if s[i]='e' then inc(dem);
writeln(f2,dem);
close(f1);
close(f2);
end.




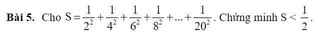






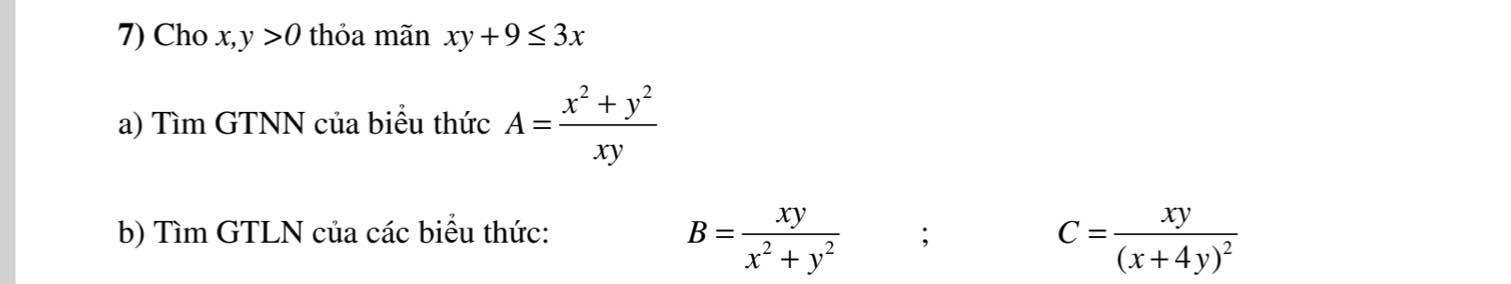 mọi người giúp em 2 ý này với ạ, em rất cảm ơn ạ 🥺
mọi người giúp em 2 ý này với ạ, em rất cảm ơn ạ 🥺
1) G/s 2 điểm đó là \(A\left(-1;y_1\right)\) và \(B\left(2;y_2\right)\)
\(\Rightarrow\hept{\begin{cases}y_1=-\left(-1\right)^2=-1\\y_2=-2^2=-4\end{cases}}\)
\(\Rightarrow A\left(-1;-1\right)\) và \(B\left(2;-4\right)\)
PT đường thẳng đó công thức là \(y=ax+b\Rightarrow\hept{\begin{cases}-a+b=-1\\2a+b=-4\end{cases}}\Leftrightarrow\hept{\begin{cases}a=-1\\b=-2\end{cases}}\)
Vậy PT đường thẳng đó là \(y=-x-2\)
2)
a) Với m = -1 : \(x^2-2\cdot\left(-1-1\right)x--1-3=0\)
\(\Leftrightarrow x^2+4x-2=0\)
\(\Leftrightarrow\left(x+2\right)^2=6\Rightarrow x=-2\pm\sqrt{6}\)
b) \(\Delta^'=\left[-\left(m-1\right)\right]^2-1\cdot\left(-m-3\right)\)
\(=m^2-2m+1+m+3=m^2-m+4>0\left(\forall m\right)\)
=> PT luôn có 2 nghiệm phân biệt với mọi m
Theo hệ thức viet: \(\hept{\begin{cases}x_1+x_2=2m-2\\x_1x_2=-m-3\end{cases}}\)
Ta có: \(x_1^2+x_2^2=14\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=14\)
\(\Leftrightarrow\left(2m-2\right)^2-2\left(-m-3\right)=14\)
\(\Leftrightarrow4m^2-8m+4+2m+6-14=0\)
\(\Leftrightarrow4m^2-6m-4=0\)
\(\Leftrightarrow2m^2-3m-2=0\)
\(\Leftrightarrow m\left(2m+1\right)-2\left(2m+1\right)=0\)
\(\Leftrightarrow\left(m-2\right)\left(2m+1\right)=0\)
\(\Rightarrow\orbr{\begin{cases}m=2\\m=-\frac{1}{2}\end{cases}}\left(tm\right)\)
Vậy \(m\in\left\{2;-\frac{1}{2}\right\}\)