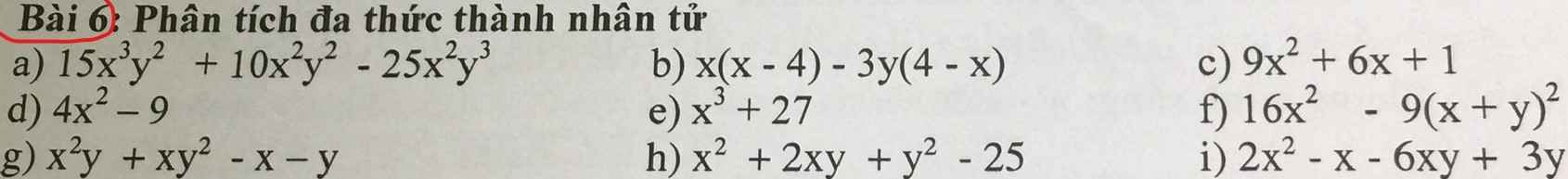phân tích đa thức thành nhân tử x2-4+3(x-2)2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
6 tháng 3 2018
Cách 1: x2 – 4 + (x – 2)2
(Xuất hiện hằng đẳng thức (3))
= (x2– 22) + (x – 2)2
= (x – 2)(x + 2) + (x – 2)2
(Có nhân tử chung x – 2)
= (x – 2)[(x + 2) + (x – 2)]
= (x – 2)(x + 2 + x – 2)
= (x – 2)(2x)
= 2x(x – 2)
Cách 2: x2 – 4 + (x – 2)2
(Khai triển hằng đẳng thức (2))
= x2 – 4 + (x2 – 2.x.2 + 22)
= x2 – 4 + x2 – 4x + 4
= 2x2 – 4x
(Có nhân tử chung là 2x)
= 2x(x – 2)
CM
22 tháng 12 2019
a) Áp dụng HĐT 1 thu được ( 2 x + y ) 2 .
b) Áp dụng HĐT 3 với A = 2x + l; B = x - l thu được
[(2x +1) + (x -1)] [(2x +1) - (x -1)] rút gọn thành 3x(x + 2).
c) Ta có: 9 - 6x + x 2 - y 2 = ( 3 - x ) 2 - y 2 = (3 - x - y)(3 -x + y).
d) Ta có: -(x + 2) + 3( x 2 - 4) = -{x + 2) + 3(x + 2)(x - 2)
= (x + 2) [-1 + 3(x - 2)] = (x + 2)(3x - 7).
12 tháng 10 2021
\(1,\\ a,=4\left(x-2\right)^2+y\left(x-2\right)=\left(4x-8+y\right)\left(x-2\right)\\ b,=3a^2\left(x-y\right)+ab\left(x-y\right)=a\left(3a+b\right)\left(x-y\right)\\ 2,\\ a,=\left(x-y\right)\left[x\left(x-y\right)^2-y-y^2\right]\\ =\left(x-y\right)\left(x^3-2x^2y+xy^2-y-y^2\right)\\ b,=2ax^2\left(x+3\right)+6a\left(x+3\right)\\ =2a\left(x^2+3\right)\left(x+3\right)\\ 3,\\ a,=xy\left(x-y\right)-3\left(x-y\right)=\left(xy-3\right)\left(x-y\right)\\ b,Sửa:3ax^2+3bx^2+ax+bx+5a+5b\\ =3x^2\left(a+b\right)+x\left(a+b\right)+5\left(a+b\right)\\ =\left(3x^2+x+5\right)\left(a+b\right)\\ 4,\\ A=\left(b+3\right)\left(a-b\right)\\ A=\left(1997+3\right)\left(2003-1997\right)=2000\cdot6=12000\\ 5,\\ a,\Leftrightarrow\left(x-2017\right)\left(8x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2017\\x=\dfrac{1}{4}\end{matrix}\right.\\ b,\Leftrightarrow\left(x-1\right)\left(x^2-16\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=4\\x=-4\end{matrix}\right.\)
24 tháng 10 2021
Bài 6:
c: \(9x^2+6x+1=\left(3x+1\right)^2\)
d: \(4x^2-9=\left(2x-3\right)\left(2x+3\right)\)
e: \(x^3+27=\left(x+3\right)\left(x^2-3x+9\right)\)
AH
Akai Haruma
Giáo viên
24 tháng 12 2021
Bài 1:
$5x+10=5(x+2)$
Bài 2:
Tại $x=8$ thì $x^2+4x+4=(x+2)^2=(8+2)^2=10^2=100$
AH
Akai Haruma
Giáo viên
24 tháng 12 2021
Bài 3:
$x^2-6x+9=x^2-2.3.x+3^2=(x-3)^2$
Bài 4:
Diện tích mảnh đất là:
$(x+5)(x-5)=24$
$\Leftrightarrow x^2-25=24$
$\Leftrightarrow x^2=49$
$\Rightarrow x=7$ (do $x>5$)
Chiều dài mảnh đất là: $x+5=7+5=12$ (m)
MS
phân tích các đa thức thành nhân tử
a) ( x2 + 4)2- 16x2
b) ( x+3)2- 8x3
c) (4x2-3x -18)2- ( 4x2 + 3x)2
1
LN
10 tháng 10 2021
\(a,\left(x^2+4\right)^2-16x^2=\left(x^2+4\right)-\left(4x\right)^2=\left(x^2+4-4x\right).\left(x^2+4+4x\right)=\left(x-2\right)^2.\left(x+2\right)^2\)
\(b,\left(x+3\right)^3-8x^3=\left(x+3\right)^3-\left(2x\right)^3=\left(x+3-2x\right).\left[x^2+\left(x+3\right).2x+\left(2x\right)^2\right]=\left(3-x\right).\left(x^2+2x^2+6x+4x^2\right)\)
\(c,\left(4x^2-3x-18\right)^2-\left(4x^2+3x\right)^2=\left(4x^2-3x-18-4x^2-3x\right).\left(4x^2-3x-18+4x^2+3x\right)=\left(-6x-18\right).\left(8x^2-18\right)\)
CM
20 tháng 10 2017
x2 + 4x – 2xy – 4y + y2 = (x2-2xy+ y2) + (4x – 4y) → bạn Việt dùng phương pháp nhóm hạng tử
= (x - y)2 + 4(x – y) → bạn Việt dùng phương pháp dùng hằng đẳng thức và đặt nhân tử chung
= (x – y)(x – y + 4) → bạn Việt dùng phương pháp đặt nhân tử chung
6 tháng 11 2021
\(1,=x\left(x^2-2x+1-y^2\right)=x\left[\left(x-1\right)^2-y^2\right]=x\left(x-y-1\right)\left(x+y-1\right)\\ 2,=\left(x+y\right)^3\\ 3,=\left(2y-z\right)\left(4x+7y\right)\\ 4,=\left(x+2\right)^2\\ 5,Sửa:x\left(x-2\right)-x+2=0\\ \Leftrightarrow\left(x-2\right)\left(x-1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)