A = 4 / 1 x 3 x5 + 4 / 3 x 5 x7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NU
4
DF
7
1 tháng 6 2019
546 + 54 = 600
1 x 2 x3 x 4 x5 x6 x7 x8 x9 = 362880
T
27 tháng 10 2023
a,
\(A=4(x-2)(x+1)+(2x-4)^2+(x+1)^2\\=[2(x-2)]^2+2\cdot2(x-2)(x+1)+(x+1)^2\\=[2(x-2)+(x+1)]^2\\=(2x-4+x+1)^2\\=(3x-3)^2\)
Thay $x=\dfrac12$ vào $A$, ta được:
\(A=\Bigg(3\cdot\dfrac12-3\Bigg)^2=\Bigg(\dfrac{-3}{2}\Bigg)^2=\dfrac94\)
Vậy $A=\dfrac94$ khi $x=\dfrac12$.
b,
\(B=x^9-x^7-x^6-x^5+x^4+x^3+x^2-1\\=(x^9-1)-(x^7-x^4)-(x^6-x^3)-(x^5-x^2)\\=[(x^3)^3-1]-x^4(x^3-1)-x^3(x^3-1)-x^2(x^3-1)\\=(x^3-1)(x^6+x^3+1)-x^4(x^3-1)-x^3(x^3-1)-x^2(x^3-1)\\=(x^3-1)(x^6+x^3+1-x^4-x^3-x^2)\\=(x^3-1)(x^6-x^4-x^2+1)\)
Thay $x=1$ vào $B$, ta được:
\(B=(1^3-1)(1^6-1^4-1^2+1)=0\)
Vậy $B=0$ khi $x=1$.
$Toru$
NT
3
NN
3
15 tháng 11 2017
a) 4 x 6 x 8 = 24 x 8 = 224
4 x 6 x 8 = 4 x 48 = 224
2 x 6 x 5 = 12 x 5 = 60
2 x 6 x 5 = 2 x 5 x 6 = 10 x 6 = 60
b) 3 x 9 x 7 = 27 x 7 = 189
3 x 9 x 7 = 3 x 63 = 189
4 x 7 x 3 = 28 x 3 = 84
4 x 7 x 3 = 4 x 21 = 84
NN
2
PT
1
CM
4 tháng 7 2018
Thu gọn, sắp xếp đa thức theo lũy thừa giảm của biến:
* Ta có: f(x) = x7 – 3x2 – x5 + x4 – x2 + 2x – 7
= x7 - (3x2+ x2) – x5+ x4 + 2x – 7
= x7 – 4x2 – x5+ x4 + 2x – 7
= x7 – x5 + x4 – 4x2 + 2x - 7
g(x) = x – 2x2 + x4 – x5 – x7 – 4x2 – 1
= x – ( 2x2 + 4x2) + x4 – x5 –x7 – 1
= x – 6x2 + x4 – x5 – x7 – 1
= -x7 – x5 + x4 – 6x2 + x – 1
* f(x) – g(x)
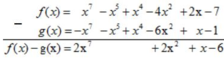
Vậy f(x) – g(x) = 2x7 + 2x2 + x - 6
\(A=\frac{4}{1.3.5}+\frac{4}{3.5.7}=\frac{4}{15}+\frac{4}{105}=\frac{28}{105}+\frac{4}{105}=\frac{32}{105}\)
Chừng nào phép tính dài hơn thì mới dùng công thức nha