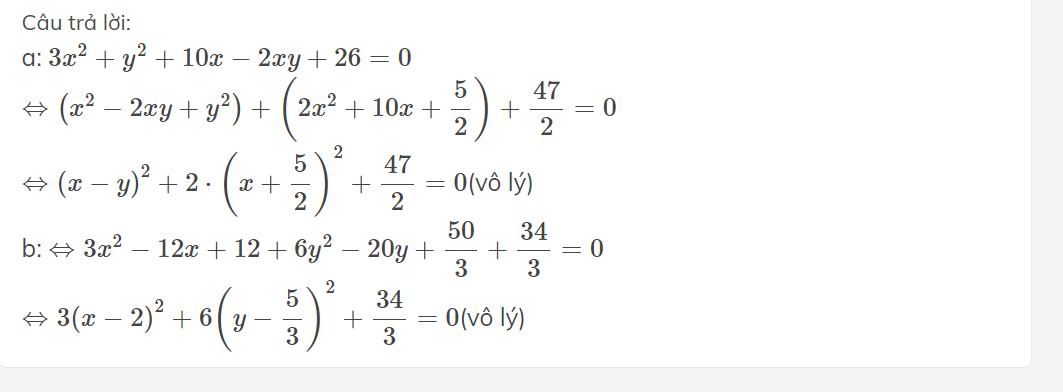Chứng minh rằng ko có giá trị nào thỏa mãn đẳng thức sau 3x^2+6y^2 -12x-20y+40=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
B
1
T
26 tháng 8 2023
\(3x^2+6y^2-12x-20y+40=0\)
\(\Rightarrow\left(3x^2-12x+12\right)+\left(6y^2-12y+6\right)+22=0\)
\(\Rightarrow3\left(x^2-4x+4\right)+6\left(y^2-2y+1\right)+22=0\)
\(\Rightarrow3\left(x-2\right)^2+6\left(y-1\right)^2+22=0\)
Ta thấy: \(3\left(x-2\right)^2\ge0\forall x\)
\(6\left(y-1\right)^2\ge0\forall y\)
\(\Rightarrow3\left(x-2\right)^2+6\left(y-1\right)^2\ge0\forall x;y\)
\(\Rightarrow3\left(x-2\right)^2+6\left(y-1\right)^2+22>0\forall x;y\)
Mặt khác: \(3\left(x-2\right)^2+6\left(y-1\right)^2+22=0\)
Suy ra: Không có giá trị nào của x; y thoả mãn yêu cầu đề bài.
#Ayumu
ML
11 tháng 8 2015
bạn c/m cho nó lớn hơn hoặc nhỏ hơn 0 đi mk ngại làm vì hơi nhìu ^.^ sory
25 tháng 8 2016
bài này chỉ có hsg như tui, alibaba nguyễn, hoàng lê bảo ngọc ..... làm dc
TN
1 tháng 10 2016
a) 4x2+3y2-4x+30y+78
=4x2-4x+1+3y2+30y+75+2
=(4x2-4x+1)+3(y2+10y+25)+2
=(2x-1)2+3(y+5)2+2>0 với mọi x
=>ko có x;y nào thỏa mãn
b)3x2+6y2-12x-20y+40
\(=3\left(x^2-4x+4\right)+6\left(y^2-\frac{10}{3}+\frac{25}{9}\right)+\frac{34}{3}\)
\(=3\left(x-2\right)^2+6\left(y-\frac{5}{3}\right)^2+\frac{34}{3}>0\) với mọi x
=>ko có x;y nào thỏa mãn
30 tháng 1 2022
a: \(3x^2+y^2+10x-2xy+26=0\)
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(2x^2+10x+\dfrac{5}{2}\right)+\dfrac{47}{2}=0\)
\(\Leftrightarrow\left(x-y\right)^2+2\cdot\left(x+\dfrac{5}{2}\right)^2+\dfrac{47}{2}=0\)(vô lý)
b: \(\Leftrightarrow3x^2-12x+12+6y^2-20y+\dfrac{50}{3}+\dfrac{34}{3}=0\)
\(\Leftrightarrow3\left(x-2\right)^2+6\left(y-\dfrac{5}{3}\right)^2+\dfrac{34}{3}=0\)(vô lý)
Y
23 tháng 8 2018
Bài a:
1) \(x^2+4y^2-4x-4y+2016\)
\(=\left(x^2-4x+4\right)+\left(4y^2-4y+1\right)+2011\)
\(=\left(x-2\right)^2+\left(2y-1\right)^2+2011\)
Vì \(\left(x-2\right)^2\ge0\)
\(\left(2y-1\right)^2\ge0\)
\(2011>0\)
\(\Rightarrow\left(x-2\right)^2+\left(2y-1\right)^2+2011>0\)
Vậy biểu thức trên luôn dương với mọi giá trị của biến
2) \(4x^2+4xy+17y^2-8y+1\)
\(=\left(4x^2+4xy+y^2\right)+\left(16y^2-8y+1\right)\)
\(=\left(2x+y\right)^2+\left(4y-1\right)^2\)
Vì \(\left(2x+y\right)^2\ge0\)
\(\left(4y-1\right)^2\ge0\)
\(\Rightarrow\left(2x+y\right)^2+\left(4y-1\right)^2\ge0\)
Vậy biểu thức trên luôn dương với mọi giá trị của biến
3) \(2x^2-5x+13\)
\(=2\left(x^2-\dfrac{5}{2}x+\dfrac{13}{2}\right)\)
\(=2\left(x^2-2.x.\dfrac{5}{4}+\dfrac{25}{16}-\dfrac{25}{16}+\dfrac{13}{2}\right)\)
\(=2\left(x-\dfrac{5}{4}\right)^2+\dfrac{79}{8}\)
Vì \(2\left(x-\dfrac{5}{4}\right)^2\ge0\)
\(\dfrac{79}{8}>0\)
\(\Rightarrow2\left(x-\dfrac{5}{4}\right)^2+\dfrac{79}{8}>0\)
Vậy biểu thức trên luôn dương với mọi giá trị của biến x
Bài b:
1) \(3x^2+y^2+10x-2xy+26=0\)
\(\Rightarrow\left(x^2-2xy+y^2\right)+\left(2x^2+10x+26\right)=0\)
\(\Rightarrow\left(x-y\right)^2+2\left(x^2+5x+13\right)=0\)
\(\Rightarrow\left(x-y\right)^2+2\left(x^2+2.x.\dfrac{5}{2}+\dfrac{25}{4}-\dfrac{25}{4}+13\right)=0\)
\(\Rightarrow\left(x-y\right)^2+2\left(x+\dfrac{5}{2}\right)^2+\dfrac{27}{2}=0\)
Vì \(\left(x-y\right)^2\ge0\)
\(2\left(x+\dfrac{5}{2}\right)^2\ge0\)
\(\dfrac{27}{2}>0\)
\(\Rightarrow\left(x-y\right)^2+2\left(x+\dfrac{5}{2}\right)^2+\dfrac{27}{2}>0\)
Vậy không có các số x,y thỏa mãn đẳng thức trên
2) \(3x^2+6y^2-12x-20y+40=0\)
\(\Rightarrow\left(3x^2-12x+12\right)+\left(6y^2-20y\right)+40=0\)
\(\Rightarrow3\left(x^2-4x+4\right)+6\left(y^2-\dfrac{3}{10}y\right)+28=0\)
\(\Rightarrow3\left(x-2\right)^2+6\left(y^2-2.y.\dfrac{3}{20}+\dfrac{9}{400}-\dfrac{9}{400}\right)+28=0\)
\(\Rightarrow3\left(x-2\right)^2+6\left(y-\dfrac{3}{20}\right)^2-\dfrac{27}{200}+28=0\)
\(\Rightarrow3\left(x-2\right)^2+6\left(y-\dfrac{3}{20}\right)^2+\dfrac{5573}{200}=0\)
Vì \(3\left(x-2\right)^2\ge0\)
\(6\left(y-\dfrac{3}{20}\right)^2\ge0\)
\(\dfrac{5573}{200}>0\)
\(\Rightarrow3\left(x-2\right)^2+6\left(y-\dfrac{3}{20}\right)^2+\dfrac{5573}{200}>0\)
Vậy biểu thức trên không có giá trị x,y thỏa mãn
H
0
18 tháng 11 2016
\(x^2+4y^2+z^2-2x+8y-6z+15=0\)
\(\Leftrightarrow\left(x^2-2x+1\right)+\left(4y^2+8y+4\right)+\left(z^2-6z+9\right)+1=0\)
\(\Leftrightarrow\left(x-1\right)^2+\left(2y+2\right)^2+\left(z-3\right)^2+1=0\)
Mà ta có
\(\hept{\begin{cases}\left(x-1\right)^2\ge0\\\left(2y+2\right)^2\ge0\\\left(z-3\right)^2\ge0\end{cases}}\)
\(\Rightarrow\left(x-1\right)^2+\left(2y+2\right)^2+\left(z-3\right)^2+1>0\)
Vậy không tồn tại x, y, z thỏa mãn đẳng thức trên