một xí nghiệp đặt 3000 sản phẩm trong 1 thời gian nhất định. Trong 6 ngày đầu họ thực hiện đúng tiến độ, mỗi ngày sau đó vượt 10 sp nên không hoàn thành sớm đc 1 ngày mà còn vượt mức 60 sản phẩm.Tính năng suất dự kiến của xí nghiệp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 2 2017
Gọi số sản phẩm nhóm thợ theo kế hoạch phải làm mỗi ngày là x (x ∈ ℕ * )
+) Theo kế hoạch: Thời gian hoàn thành là 3000/x (ngày)
+) Thực tế:
Số sản phẩm làm trong 8 ngày là 8x (sản phẩm)
Số sản phẩm còn lại là 3000 – 8x (sản phẩm)
Mỗi ngày sau đó nhóm thợ làm được x + 10 (sản phẩm)
Thời gian hoàn thành 3000 - 8 x x + 10 (ngày)
Vì thời gian thực tế ít hơn thời gian dự định là 2 ngày nên ta có phương trình:
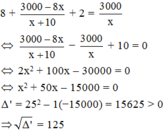
Phương trình có hai nghiệm phân biệt: x 1 = − 25 – 125 = −150 (loại) và
x 2 = −25 + 125 = 100 (tmđk)
Vậy theo kế hoạch, mỗi ngày cần làm 100 sản phẩm
Đáp án: A
6 tháng 4 2023
Gọi thời gian dự kiến là x
=>Số sản phẩm theo kế hoạch là 50x
Số sản phẩm thực tế là (x-3)*65
Theo đề, ta có: (x-3)*65-50x=255
=>15x-195=255
=>15x=450
=>x=30
=>Số sản phẩm dự kiến là 450sp
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 3 2021
Gọi số sản phẩm làm theo kế hoạch mỗi ngày là x>0 và số ngày dự định là y>0
Ta có: \(xy=200\)
4 ngày đầu làm được: \(4x\) sản phẩm
Những ngày còn lại: \(\left(y-6\right)\left(x+10\right)\)
Theo bài ra ta có hệ:
\(\left\{{}\begin{matrix}xy=200\\4x+\left(y-6\right)\left(x+10\right)=200\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy=200\\5y-x=30\end{matrix}\right.\)
\(\Rightarrow y\left(5y-30\right)=200\)
\(\Leftrightarrow y^2-6y-40=0\Rightarrow\left[{}\begin{matrix}y=10\\y=-4\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow x=\dfrac{200}{10}=20\)
HL
30 tháng 6 2019
#) Giải
+) Gọi số ngày mà xí nghiệp đã hoàn thành công việc là x ( x>0, ngày )
- Theo dự định, trong một ngày, xí nghiệp sản xuất đựoc số sản phẩm là 1500 : 30 = 50 (sản phẩm )
-Trên thực tế, trong một ngày, xí nghiệp sản xuất được số sản phẩm là 50 + 15 = 65 ( sản phẩm )
+) Theo đề bài ta có phương trình :
65x = 1500 + 255
<=> 65x = 1755
<=> x =1755 : 65 =27 (ngày )
=> Thực tế, xí nghiệp đã rút ngắn được số ngày là 30 - 27 = 3 ( ngày )
Đ/s: 3 ngày
~ Hok tốt ~
HH
7 tháng 6 2020
Bài này có 2 cách nha bạn :)
*Cách 1 :
Số sản phẩm trong một ngày theo dự định ban đầu là \(\frac{1500}{30}=50\)( sản phẩm )
Thực tế, mỗi ngày xí nghiệp sản xuất được: 50 + 15 =65 (sản phẩm)
Tổng số sản phẩm thực tế xí nghiệm sản xuất được: 1500 + 255 = 1755 (sản phẩm)
Thời gian thực tế xí nghiệm sản xuất là: 1755 : 65 = 27 (ngày)
Vậy số ngày được rút ngắn so với dự định là: 30 – 27 = 3 (ngày).
* Cách 2 :
Gọi số ngày rút bớt là x ngày : ( 0 < x < 30 )
Số sản phẩm trong một ngày theo dự định ban đầu là \(\frac{1500}{30}=50\)( sản phẩm )
Tổng số sản phẩm sản xuất được sau khi đã tăng năng suất là:
1500 + 255 =1755 (sản phẩm)
Thời gian xí nghiệp hoàn thành công việc trên thực tế là: 30−x (ngày)
Số sản phẩm sản xuất trong một ngày trên thực tế là:
\(\frac{1755}{30-x}\)( sản phẩm )
Theo đề bài, thực tế đã sản xuất mỗi ngày vượt 15 sản phẩm, nên ta có phương trình :
\(\frac{1755}{30-x}-50=15\)
\(\Leftrightarrow\frac{1755}{30-x}=50+15\)
\(\Leftrightarrow\frac{1755}{30-x}=65\)
\(\Leftrightarrow\frac{1755}{30-x}=\frac{65\left(30-x\right)}{30-x}\)
\(\Rightarrow1755=65\left(30-x\right)\)
\(\Leftrightarrow1755=1950-65x\)
\(\Leftrightarrow65x=1950-65x\)
\(\Leftrightarrow65x=195\)
\(\Leftrightarrow x=3\)( thỏa mãn đk )
Vậy xí nghiệp đã rút ngắn thời gian được 3 ngày.