
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 2.
Tóm tắt: \(m=2kg;\Delta l=10cm;g=10\)m/s2
\(F_{đh}=?;k=?\)
Bài giải:
Lực đàn hồi:
\(F=P=mg=2\cdot10=20N\)
Hệ số lực đàn hồi:
\(k=\dfrac{F}{\Delta l}=\dfrac{20}{0,1}=200\)N/m


Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{1}{2}\\x_1x_2=-2\end{matrix}\right.\)
\(A=3-x_1^2-x_2^2\\ =3-\left(x_1^2+x_2^2\right)\\ =3-\left[\left(x_1+x_2\right)^2-2x_1x_2\right]\\ =3-\left[\left(-\dfrac{1}{2}\right)^2-2.\left(-2\right)\right]\\ =3-\left(\dfrac{1}{4}+4\right)\\ =3-\dfrac{17}{4}\\ =-\dfrac{5}{4}\)
\(B=\left(x_1-x_2\right)^2\\ =x_1^2+x_2^2-2x_1x_2\\ =\left(x_1+x_2\right)^2-4x_1x_2\\ =\left(\dfrac{1}{2}\right)^2-4.\left(-2\right)\\ =\dfrac{1}{4}+8\\ =\dfrac{33}{4}\)
\(D=\left(1+x_1\right)\left(2-x_1\right)+\left(1+x_2\right)\left(2-x_2\right)\\ =2+x_1-x_1^2+2+x_2-x_2^2\\ =4+\left(x_1+x_2\right)-\left(x_1^2+x_2^2\right)\\ =4+\dfrac{1}{2}-\left[\left(x_1+x_2\right)^2-2x_1x_2\right]\\ =\dfrac{9}{2}-\left[\left(\dfrac{1}{2}\right)^2-2.\left(-2\right)\right]\\ =\dfrac{9}{2}-\dfrac{17}{4}\\ =\dfrac{1}{4}\)


- 1999 . 19981998 + 19991999 . 1998
= - 1999 . 1998 . 10001 + 1999 . 10001 . 1998
= 10001 . 1998 ( - 1999 + 1999 )
= 10001 . 1998 . 0
= 0


25. Hợp chất khí với H của 1 nguyên tố là \(RH_3\)
=> Chọn C. Oxit cao nhất của R là \(R_2O_5\), oxit axit
26. R nằm ở nhóm IA
=> Chọn B. R có tính kim loại
27. Cấu hình e: \(1s^22s^22p^63s^23p^2\)
=> R thuộc nhóm IVA
=> Công thức oxit cao nhất: \(RO_2\)
=> Chọn C

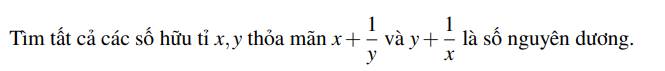 giup minh vs minh cam on a
giup minh vs minh cam on a



\(BH=\frac{AB^2}{BC}=\frac{3^2}{6}=1,5\left(cm\right)\)
\(AC=\sqrt{BC^2-AB^2}=\sqrt{6^2-3^2}=3\sqrt{3}cm\).
\(AH=\frac{AB.AC}{BC}=\frac{3\sqrt{3}}{2}\left(cm\right)\)
Gọi \(D,E\)lần lượt là giao điểm của đường tròn \(\left(H\right)\)với \(AB,BC\).
\(\widehat{HDB}=\widehat{HBD}=arccos\frac{3}{6}=60^o\Rightarrow\Delta HBD\)đều.
Diện tích quạt \(HBD\)là: \(\frac{60}{360}.\pi.BH^2=\frac{1}{6}.3,14.1,5^2=1,1775\left(cm^2\right)\)
DIện tích tam giác \(HBD\)là: \(\frac{1,5^2\sqrt{3}}{4}=\frac{9\sqrt{3}}{16}\left(cm^2\right)\)
Diện tích phần không màu nằm ngoài hình tam giác là: \(1,1775-\frac{9\sqrt{3}}{16}\left(cm^2\right)\)
Diện tích phần không màu nằm trong hình tam giác là:
\(\frac{1}{2}.\pi.1,5^2-\left(1,1775-\frac{9\sqrt{3}}{16}\right)cm^2\).
Diện tích tam giác là: \(\frac{1}{2}.3.3\sqrt{3}=\frac{9\sqrt{3}}{2}\left(cm^2\right)\)
Diện tích phần tô đậm là: \(\frac{9\sqrt{3}}{2}-\left[\frac{1}{2}.\pi.1,5^2-\left(1,1775-\frac{9\sqrt{3}}{16}\right)\right]\approx4,5\left(cm^2\right)\)