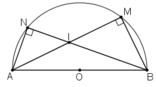
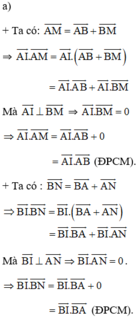Cho nửa đường tròn (O) có tâm O và đường kính AB=2R. Gọi M, N là hai điểm di động trên nửa đường (O) sao cho M thuộc cung AN và tổng khoảng cách từ A, B đến MN bằng \(R\sqrt{3}\). Gọi I là giao điểm của các đường thẳng AN và BM; K là giao điểm của AM và BN.
a) Chứng minh K, M, I, N cùng thuộc một đường tròn (C).
b) Tính độ dài MN và bán kính đường (C) theo R
c) Xác định vị trí M, N sao cho tam giác KAB có diện tích lớn nhất. Tính giá trị lớn nhất đó theo R.


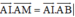 và
và 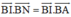
 theo R.
theo R.