Tìm giá trị của m để đa thức Q(x)=x3 +4x2 - mx-10 có 1 nghiệm là -1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.\(P\left(x\right)=1+3x^5-4x^2+x^5+x^3-x^2+3x^3\)
\(=1-5x^2+4x^3+4x^5\)
\(Q\left(x\right)=2x^5-x^2+4x^5-x^4+4x^2-5x\)
\(=-5x+3x^2+3x^4+2x^5\)
b.\(P\left(x\right)+Q\left(x\right)=1-5x^2+4x^3+4x^5-5x+3x^2+3x^4+2x^5\)
\(=6x^5+3x^4+4x^3-2x^2-5x+1\)
\(P\left(x\right)-Q\left(x\right)=1-5x^2+4x^3+4x^5+5x-3x^2-3x^4-2x^5\)
\(=2x^5-3x^4+4x^3-8x^2+5x+1\)
c.\(P\left(x\right)+Q\left(x\right)=6x^5+3x^4+4x^3-2x^2-5x+1\)
\(x=-1\)
\(P\left(x\right)+Q\left(x\right)=6.\left(-1\right)^5+3.\left(-1\right)^4+4.\left(-1\right)^3-5.\left(-1\right)+1\)
\(=-6+3-4+5+1=-1\)
d.\(Q\left(0\right)=\)\(-5x+3x^2+3x^4+2x^5\)
\(=0\)
\(P\left(0\right)=\)\(1-5x^2+4x^3+4x^5\)
\(=1\)
Vậy x=0 ko là nghiệm của đa thức P(x)

a: \(A=\left(2x-1\right)\left(4x^2+2x+1\right)-7\left(x^3+1\right)\)
\(=\left(2x\right)^3-1^3-7x^3-7\)
\(=8x^3-1-7x^3-7=x^3-8\)
b: Thay x=-1/2 vào A, ta được:
\(A=\left(-\dfrac{1}{2}\right)^3-8=-\dfrac{1}{8}-8=-\dfrac{65}{8}\)

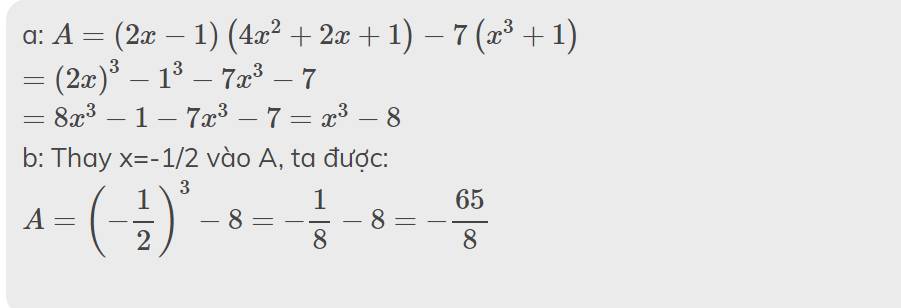
c: \(A=x^3-8=\left(x-2\right)\left(x^2+2x+4\right)\)
Để A là số nguyên tố thì x-2=1
=>x=3

bạn chỉ cần thế nghiệm vào rồi tính m là đc rồi

a) Thay x = 1 vào M(x), ta được:
\(M\left(x\right)=m.1^2+2m.1-6=m+2m-6=3m-6=0\)
\(\Leftrightarrow3m=6\Leftrightarrow m=2\)
Vậy m = 2 thì M(x) có nghiệm bằng 1
Vì x = -1 là nghiệm của đa thức Q(x)
\(\Rightarrow Q\left(-1\right)=\left(-1\right)^3+4.\left(-1\right)^2-m\left(-1\right)-10=0\)
\(\Leftrightarrow\left(-1\right)+4-\left(-m\right)-10=0\)
\(\Leftrightarrow3+m-10=0\)
\(\Leftrightarrow m-10=-3\)
\(\Leftrightarrow m=7\)
Vậy với m = 7 thì đa thức Q(x) = x3 + 4x2 - mx - 10 có nghiệm là x = -1