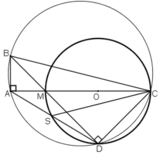
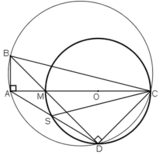
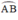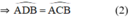Cho tam giác ABC vuông tại A, M thuộc AC. Vẽ đường tròn đường kính MC Cắt BM tại D và cắt BC tại N. Gọi S là Giao điểm của BA va CD.
a/ Chứng minh: tứ giác ABCD nội tiếp.
b/ Chứng minh BD là phân giác của góc ADN.
c/ Chứng minh SM vuông với BC và ba điểm S,M,N thẳng hàng

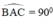 ⇒ A ∈ đường tròn đường kính BC.
⇒ A ∈ đường tròn đường kính BC.
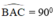 ⇒ A ∈ đường tròn đường kính BC.
⇒ A ∈ đường tròn đường kính BC.
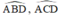 đều là góc nội tiếp chắn cung
đều là góc nội tiếp chắn cung 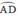
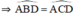
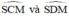 đều là các góc nội tiếp cùng chắn cung
đều là các góc nội tiếp cùng chắn cung 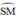
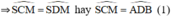
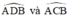 đều là các góc nội tiếp chắn cung
đều là các góc nội tiếp chắn cung