Cho tam giác ABC có AB = AC =15cm, BC = 24cm. Gọi M là trung điểm của BC.
A) Tính AM
B) Gọi G là trọng tâm của tam giác ABC. Tính AG ?
*Mọi người giúp em với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. áp dụng dl Pytago ta có
BC^2= AB^2+AC^2
BC^2= 8^2+15^2=64+225=289(cm)
=> BC= căn 289=17cm
b. vì trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng 1/2 cạnh huyền nên
AM= 1/2BC= BC/2=8.5cm
AG= 2/3 AM = 2/3 . 8.5 xấp xỉ 5.7

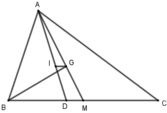
Gọi D, M là giao điểm của AI, AG với BC.
Vì AD là tia phân giác góc B A C ^ nên B D A B = D C A C (t/c)
⇒ B D 12 = D C 18 = B D + D C 12 + 18 = 15 30 = 1 2
=> BD = 12. 1 2 = 6, DC =18. 1 2 = 9
Lại có: BI là tia phân giác A B D ^ nên A I I D = A B B D = 12 6 = 2 (tính chất)
=> I D A D = M G M A = 1 3 hay D đúng
Mà AG = 2GM (vì G là trọng tâm)
Nên A I I D = A G G M = 2 hay B đúng
Theo định lí đảo của định lí Talet ta có:
IG // DM => IG // BC hay A đúng
Chỉ có C sai
Đáp án: C

a) Xét tam giác ABC vuông tại A, áp dụng định lý Pytago ta có :
\(BC^2=AB^2+AC^2=5^2+12^2=25+144=169=13^2\)
Mà BC>0 nên BC = 13 cm.
Vậy BC = 13 cm.
b) AM là đường trung tuyến ứng với cạnh huyền nên \(AM=\frac{1}{2}BC=\frac{13}{2}=6,5\)(cm)
Vậy AM = 6,5 cm.
c) G là trọng tâm tam giác nên ta có \(AG=\frac{2}{3}AM=\frac{2}{3}.6,5=\frac{13}{3}\)(cm)
Vậy AG = 13/3 cm.

có AB=AC suy ra tam giác ABC cân
mà AE là phân giác góc BAC suy ra AE là đg cao (tính chất)và cũng suy ra b)AE là đg trung trực của BC
xét 2 tam giác vuông ABE và ACE co
suy ra 2 tam giác bằng nhau
a: Xet ΔABE và ΔACE có
AB=AC
góc BAE=góc CAE
AE chung
=>ΔABE=ΔACE
b: ΔABC cân tại A
mà AE là phân giác
nên AE là trung tuyến
c: ΔABC cân tại A
mà AE là trung tuyến
nên AE vuông góc BC
d: AG=2/3*AE=6cm
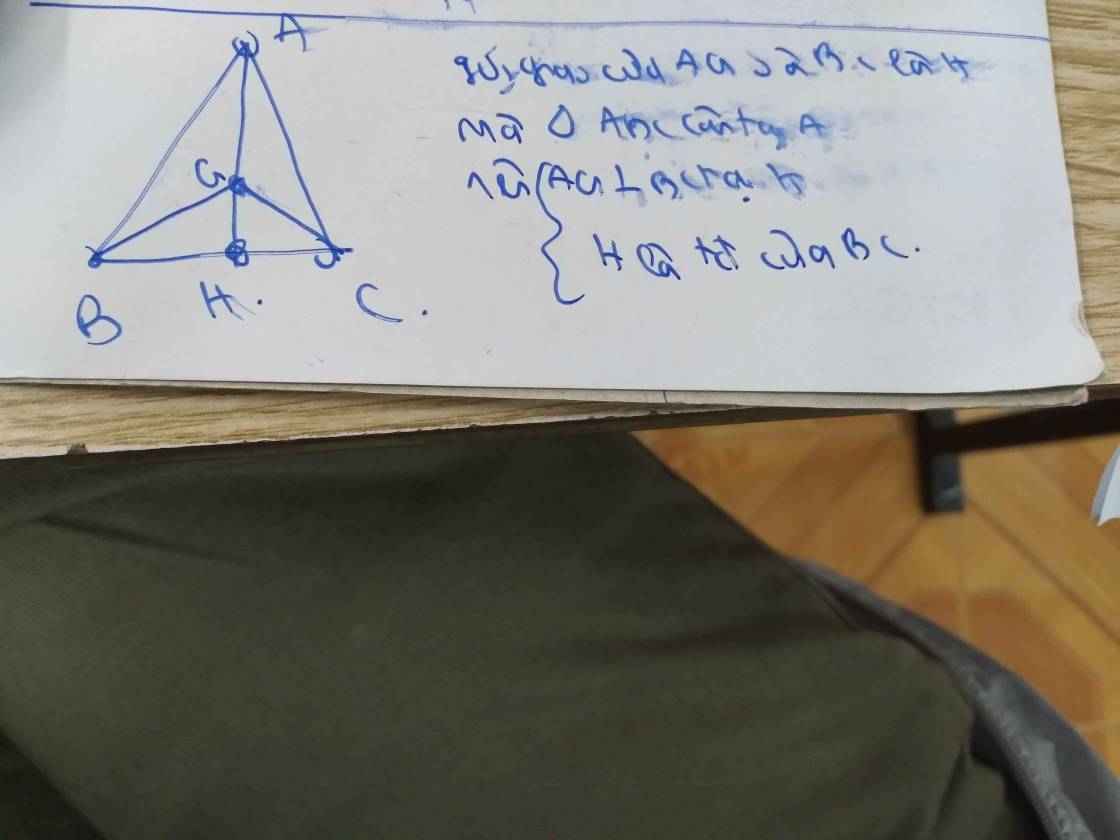

Giải:
a) Ta có: MB=MC = 1/2 BC = 1/2 * 24 = 12(CM)
Tam giác ABC vuông tại A, theo định lí Py-ta-go, ta có:
AM2 = AB2 - MB2 = 152 - 122 = 81
AM = \(\sqrt{81}\)= 9(cm)
b) G là trọng tâm cùa tam giác ABC
Suy ra AG = 2/3 * AM = 2/3 * 9 = 6(cm)
Cảm ơn bn ạ