Công thức nghiệm pt bậc 2 và hằng đẳng thức
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


9:Chứng minh cho bốn đỉnh của tứ giác cách đều một điểm nào đó
Chứng minh tứ giác có tổng 2 góc đối bằng 180°
Chứng minh từ hai đỉnh cùng kề một cạnh cùng nhìn một cạnh dưới hai góc bằng nhau. Nếu một tứ giác có tổng số đo hai góc đối bằng thì tứ giác đó nội tiếp được trong một đường tròn.

(6) (a+b+c)3=a3+b3+c3+3(a+b)(b+c)(c+a)(a+b+c)3=a3+b3+c3+3(a+b)(b+c)(c+a)
(7) a3+b3+c3−3abc=(a+b+c)(a2+b2+c2−ab−bc−ac)a3+b3+c3−3abc=(a+b+c)(a2+b2+c2−ab−bc−ac)
(8) (a−b)3+(b−c)3+(c−a)3=3(a−b)(b−c)(c−a)(a−b)3+(b−c)3+(c−a)3=3(a−b)(b−c)(c−a)
(9) (a+b)(b+c)(c+a)−8abc=a(b−c)2+b(c−a)2+c(a−b)2(a+b)(b+c)(c+a)−8abc=a(b−c)2+b(c−a)2+c(a−b)2
(10) (a+b)(b+c)(c+a)=(a+b+c)(ab+bc+ca)−abc(a+b)(b+c)(c+a)=(a+b+c)(ab+bc+ca)−abc
(11) ab2+bc2+ca2−a2b−b2c−c2a=(a−b)3+(b−c)3+(c−a)33ab2+bc2+ca2−a2b−b2c−c2a=(a−b)3+(b−c)3+(c−a)33
(12)ab3+bc3+ca3−a3b−b3c−c3a=(a+b+c)[(a−b)3+(b−c)3+(c−a)3]3ab3+bc3+ca3−a3b−b3c−c3a=(a+b+c)[(a−b)3+(b−c)3+(c−a)3]3
(13) an−bn=(a−b)(an−1+an−2b+an−3b2+...+a2bn−3+abn−2+bn−1)an−bn=(a−b)(an−1+an−2b+an−3b2+...+a2bn−3+abn−2+bn−1)
(14) Với n lẻ:
an+bn=(a+b)(an−1−an−2b+an−3b2−...+a2bn−3−abn−2+bn−1)an+bn=(a+b)(an−1−an−2b+an−3b2−...+a2bn−3−abn−2+bn−1)
(15) Nhị thức Newton:
(a+b)n=an+n!(n−1)!1!an−1b+n!(n−2)!2!an−2b2+...+n!(n−k)!k!an−kbk+...+n!2!(n−2)!a2bn−2+n)!1!(n−1)!abn−1+bn

Căn bậc hai số học của một số nguyên dương x là a sao cho
\(\left\{{}\begin{matrix}a>0\\a^2=x\end{matrix}\right.\)
Hằng đẳng thức về căn thức là:
\(\sqrt{A^2}=\left|A\right|\)
Quy tắc:
\(\sqrt{A^2\cdot B}=\sqrt{B}\cdot\left|A\right|\)
\(\sqrt{\dfrac{A}{B}}=\dfrac{\sqrt{A}}{\sqrt{B}}\)
\(\sqrt{A\cdot B}=\sqrt{A}\cdot\sqrt{B}\)


a) Các hằng đẳng thức lượng giác cơ bản:
sin2α + cos2α = 1
1 + tan2α = 1/(cos2α); α ≠ π/2 + kπ, k ∈ Z
1 + cot2α = 1/(sin2α); α ≠ kπ, k ∈ Z
tanα.cotα = 1; α ≠ kπ/2, k ∈ Z
b) Công thức cộng:
cos(a - b) = cosa cosb + sina sinb
cos(a + b) = cosa cosb - sina sinb
sin(a - b) = sina cosb - cosa sinb
sin(a + b) = sina.cosb + cosa.sinb
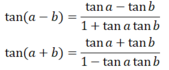
c) Công thức nhân đôi:
sin2α = 2 sinα cosα
cos2α = cos2α - sin2α = 2cos2α - 1 = 1 - 2sin2α
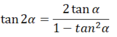
d) Công thức biến đổi tích thành tổng:
cos a cosb = 1/2 [cos(a - b) + cos(a + b) ]
sina sinb = 1/2 [cos(a - b) - cos(a + b) ]
sina cosb = 1/2 [sin(a - b) + sin(a + b) ]
Công thức biến đổi tổng thành tích:
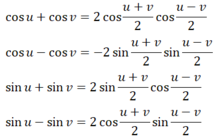

dể đa thức x^2 +2x +2 có nghiệm nên suy ra x thuộc ước của 2
thay x lần lượt suy ra pt vô nghiệm
Bài này bn phải phân tích ra đưa về dạng 1 hằng đẳng thức(=(x+1)2) rồi suy ra vô nghiệm, ko nên giải theo cách khác

= (x+1-y)(x+1+y)
hằng đẳng thức số 3: a^2 - b^2 = (a-b)(a+b)
\(\left(x+1\right)^2-y^2=\left(x+1-y\right)\left(x+1+y\right)\)

công thức :
6.tổng hai lập phương :
A3 + B3 = ( A+B).(A2 - AB + B2 )
7. hiệu hai lập phương :
A3 - B3 = ( A-B).( A2+ AB + B2 )
*Sxl
công thức 6.Tổng 2 lập phương
với a và b là biểu thức tùy ý ta có:A3+B3 =(A+B)(A2-AB+B2)
công thức 7:hiệu 2 lập phuong
A3-B3=(A-B)(A2+AB+B2)