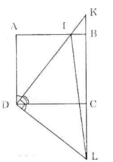
Bài 1)cho hình vuông ABCD , gọi I là một điểm trong đoạn AB. Tia DI cắt tia CB ở K. Dx vuông góc với DK và cắt đường thẳng BC tại L. CM:a) Tam giác DIL cânb)1/Di2 +1/DK2 không đổi khi I di động trên đoạn ABBài 2) cho một tam giác vuông ABC vuông góc tại A và đường cao AH. Từ H kẻ HF vuông góc với AC và HE vuông góc với AB (F thuộc AC và E thuộc AB ) 1) tứ giác AEHF là hình gì?2) CM các hệ thức :a) AE.AB...
Đọc tiếp
Bài 1)cho hình vuông ABCD , gọi I là một điểm trong đoạn AB. Tia DI cắt tia CB ở K. Dx vuông góc với DK và cắt đường thẳng BC tại L. CM:
a) Tam giác DIL cân
b)1/Di2 +1/DK2 không đổi khi I di động trên đoạn AB
Bài 2) cho một tam giác vuông ABC vuông góc tại A và đường cao AH. Từ H kẻ HF vuông góc với AC và HE vuông góc với AB (F thuộc AC và E thuộc AB )
1) tứ giác AEHF là hình gì?
2) CM các hệ thức :a) AE.AB = AF.AC
b)BH.HC=4EO.OF
là không đổi.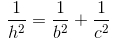
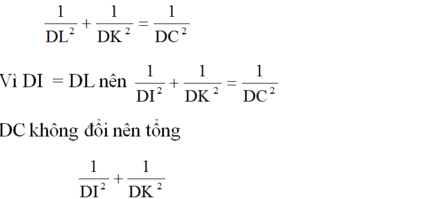
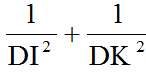
Bài 2)
1) xét tứ giác AEHF có góc A=90* F=90* E=90* (GT)
==)) AEHF Là hình chữ nhật
2) Vì AEHF là hình chữ nhật ==)) EF=AH(đl) gọi O là giao điểm của EF và AH
==))EO=OF=AO=OH
EO=AO ==)) tam giác EOA cân tại O,==)) OEA=góc OAE
mà góc OAE=góc BCA (cùng phụ với góc HAC ) ==))góc OEA =góc BCA(1)
góc A=90* chung ==)) tam giác EAF~tam giác CAB (g-g)
==))EA/CA=AF/AB ==))AE.AB=AF.AC
2)ta có BH.HC=AH2
AH2=( AO+OH )2=AO2+OH2+2AO.OH mà AO=OH ==))AH2=4.OA2
4EO.OF=4OE2 mà OE=OA(cmt)==))4EO.OF=AH2=BH.HC