giải phương trình (x^2-2x+1)-4=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 12 2021
anh ơi, vậy là sai đề hả anh, chứ đề kêu chứng minh phương trình vô nghiệm mà em thấy anh ghi x=2
S
23 tháng 2 2021
Mình khuyên bạn thế này :
Bạn nên tách những câu hỏi ra
Như vậy các bạn sẽ dễ giúp
Và cũng có nhiều bạn giúp hơn !
23 tháng 2 2021
Bài 1.
a) ( x - 3 )( x + 7 ) = 0
<=> x - 3 = 0 hoặc x + 7 = 0
<=> x = 3 hoặc x = -7
Vậy S = { 3 ; -7 }
b) ( x - 2 )2 + ( x - 2 )( x - 3 ) = 0
<=> ( x - 2 )( x - 2 + x - 3 ) = 0
<=> ( x - 2 )( 2x - 5 ) = 0
<=> x - 2 = 0 hoặc 2x - 5 = 0
<=> x = 2 hoặc x = 5/2
Vậy S = { 2 ; 5/2 }
c) x2 - 5x + 6 = 0
<=> x2 - 2x - 3x + 6 = 0
<=> x( x - 2 ) - 3( x - 2 ) = 0
<=> ( x - 2 )( x - 3 ) = 0
<=> x - 2 = 0 hoặc x - 3 = 0
<=> x = 2 hoặc x = 3
ND
Nguyễn Đức Trí
VIP
15 tháng 9 2023
1) \(-2x^2+x+1-2\sqrt[]{x^2+x+1}=0\)
\(\Leftrightarrow2\sqrt[]{x^2+x+1}=-2x^2+x+1\left(1\right)\)
Ta có :
\(2\sqrt[]{x^2+x+1}=2\sqrt[]{\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}}\ge\sqrt[]{3}\)
Dấu "=" xảy ra khi và chỉ khi \(x+\dfrac{1}{2}=0\Leftrightarrow x=-\dfrac{1}{2}\)
\(\left(1\right)\Leftrightarrow-2x^2+x+1=\sqrt[]{3}\)
\(\Leftrightarrow2x^2-x+\sqrt[]{3}-1=0\)
\(\Delta=1-8\left(\sqrt[]{3}-1\right)=9-8\sqrt[]{3}\)
\(pt\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1+\sqrt[]{9-8\sqrt[]{3}}}{4}\left(loại\right)\\x=\dfrac{1-\sqrt[]{9-8\sqrt[]{3}}}{4}\left(loại\right)\end{matrix}\right.\) \(\left(vì.x=-\dfrac{1}{2}\right)\)
Vậy phương trình cho vô nghiệm
Y
12 tháng 4 2022
\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)
\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)
\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)
\(\Leftrightarrow x^2-9-x^2+3x=0\)
\(\Leftrightarrow3x-9=0\)
\(\Leftrightarrow3x=9\)
\(\Leftrightarrow x=3\left(n\right)\)
Vậy \(S=\left\{3\right\}\)
Y
12 tháng 4 2022
\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)
\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)
\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)
\(\Leftrightarrow12x-9-12x+20+2x-7>0\)
\(\Leftrightarrow2x+4>0\)
\(\Leftrightarrow2x>-4\)
\(\Leftrightarrow x>-2\)
18 tháng 2 2021
Ta có: \(\left(x^2-2x+1\right)-4=0\)
\(\Leftrightarrow\left(x-1\right)^2-2^2=0\)
\(\Leftrightarrow\left(x-1-2\right)\left(x-1+2\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-1\end{matrix}\right.\)
Vậy: S={3;-1}
PT
2
30 tháng 4 2021
Ta có: \(\left(x^2-2x+1\right)-4=0\)
\(\Leftrightarrow\left(x-1\right)^2-2^2=0\)
\(\Leftrightarrow\left(x-1-2\right)\left(x-1+2\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+1=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-1\end{matrix}\right.\)
Vậy...
30 tháng 4 2021
Ta có: \(x^2-2x+1-4=0\)
\(\Leftrightarrow\left(x-1\right)^2=4\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=2\\x-1=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-1\end{matrix}\right.\)
Vậy: S={3;-1}
6 tháng 2 2021
\(4x^2-4x-5\left|2x-1\right|-5=0\)
\(\Leftrightarrow-5\left|2x-1\right|=5-4x^2+4x\)
\(\Leftrightarrow\left|2x-1\right|=\frac{-4x^2+4x+5}{-5}\)
\(\Leftrightarrow\left|2x-1\right|=\frac{4x\left(x-1\right)}{5}-1\)
TH1 : \(2x-1=\frac{4x\left(x-1\right)}{5}-1\Leftrightarrow2x=\frac{4x\left(x-1\right)}{5}\)
\(\Leftrightarrow10x=4x^2-4x\Leftrightarrow14x-4x^2=0\)
\(\Leftrightarrow-2x\left(2x-7\right)=0\Leftrightarrow x=0;x=\frac{7}{2}\)
TH2 : \(2x-1=-\left(\frac{4x\left(x-1\right)}{5}-1\right)\Leftrightarrow2x-1=-\frac{4x\left(x-2\right)}{5}+1\)
\(\Leftrightarrow2x-2=-\frac{4x\left(x-2\right)}{5}\Leftrightarrow10x-10=-4x^2+8x\)
\(\Leftrightarrow2x-10+4x^2=0\Leftrightarrow2\left(2x^2+x-5\ne0\right)=0\)tự chứng minh
Vậy tập nghiệm của phương trình là S = { 0 ; 7/2 }
TN
0
CM
10 tháng 2 2018
a) 2(x + 3)(x – 4) = (2x – 1)(x + 2) – 27
⇔ 2(x2 – 4x + 3x – 12) = 2x2 + 4x – x – 2 – 27
⇔ 2x2 – 2x – 24 = 2x2 + 3x – 29
⇔ -2x – 3x = 24 – 29
⇔ - 5x = - 5 ⇔ x = -5/-5 ⇔ x = 1
Tập nghiệm của phương trình : S = {1}
b) x2 – 4 – (x + 5)(2 – x) = 0
⇔ x2 – 4 + (x + 5)(x – 2) = 0 ⇔ (x – 2)(x + 2 + x + 5) = 0
⇔ (x – 2)(2x + 7) = 0 ⇔ x – 2 = 0 hoặc 2x + 7 = 0
⇔ x = 2 hoặc x = -7/2
Tập nghiệm của phương trình: S = {2; -7/2 }
c) ĐKXĐ : x – 2 ≠ 0 và x + 2 ≠ 0 (khi đó : x2 – 4 = (x – 2)(x + 2) ≠ 0)
⇔ x ≠ 2 và x ≠ -2
Quy đồng mẫu thức hai vế :
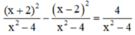
Khử mẫu, ta được : x2 + 4x + 4 – x2 + 4x – 4 = 4
⇔ 8x = 4 ⇔ x = 1/2( thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = {1/2}
d) ĐKXĐ : x – 1 ≠ 0 và x + 3 ≠ 0 (khi đó : x2 + 2x – 3 = (x – 1)(x + 3) ≠ 0)
⇔ x ≠ 1 và x ≠ -3
Quy đồng mẫu thức hai vế :
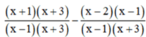
Khử mẫu, ta được : x2 + 3x + x + 3 – x2 + x – 2x + 2 + 4 = 0
⇔ 3x = -9 ⇔ x = -3 (không thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = ∅
PN
15 tháng 5 2021
\(2\left(x+3\right)\left(x-4\right)=\left(2x-1\right)\left(x+2\right)-27\)
\(< =>2\left(x^2-x-12\right)=2x^2+3x-2-27\)
\(< =>2x^2-2x-24=2x^2+3x-2-27\)
\(< =>5x=-24+29=5\)
\(< =>x=\frac{5}{5}=1\)
\(\left(x^2-2x+1\right)-4=0\)
\(\Leftrightarrow\left(x-1\right)^2-2^2=0\)
\(\Leftrightarrow\left(x-1-2\right)\left(x-1+2\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-3=0\\x+1=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=3\\x=-1\end{cases}}\)
Vậy phương trình có tập nghiệp \(S=\left\{3;-1\right\}\)