so sánh: 3^152 và 4 ^112
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
0
NT
2
16 tháng 2 2020
\(S=1+3^2+3^4+...+3^{100}\)
\(\Rightarrow9S=3^2+3^4+....+3^{102}\)
\(\Rightarrow9S-S=\left(3^2+....+3^{102}\right)-\left(1+....+3^{100}\right)\)
\(\Rightarrow8S=3^{102}-1=9^{51}-1>8^{51}:2=2^{152}\)
2 tháng 11 2015
2241=2.2240=2.215.16>( 22)7.16=47.16>37.16= 3112
Vậy 2241> 3112
VP
1
3 tháng 5 2018
a) ta có: -152/151>-153/151>-153/152
=>-152/151>-153/152
b)ta có: 1-3213/3214=1/3214
1-9875/9876=1/9876
Vì 1/3214>1/9876
=>3213/3214<9875/9876
NT
Cho A = 1/1×2 + 1/3×4 + 1/5×6 +...+ 1/217×218 và B = 1/110 + 1/111 + 1/112 +...+ 1/218
So sánh A và B
0
26 tháng 3 2022
\(A=\frac{1}{151}+\frac{1}{152}+...+\frac{1}{200}\) ( Gồm 50 số hạng )
Ta thấy \(\frac{1}{151}>\frac{1}{152}>...>\frac{1}{200}\)
\(\Rightarrow\frac{1}{151}+\frac{1}{152}+...+\frac{1}{200}>\frac{1}{200}\times50\)
\(\Rightarrow\frac{1}{151}+\frac{1}{152}+...+\frac{1}{200}>\frac{50}{200}=\frac{1}{4}\)
\(\Rightarrow A>\frac{1}{4}\)
Vậy \(A>\frac{1}{4}\)
_HT_
PD
2
24 tháng 4 2021
\(A=\frac{1}{151}+\frac{1}{152}+...+\frac{1}{200}>\frac{1}{200}+\frac{1}{200}+...+\frac{1}{200}=\frac{50}{200}=\frac{1}{4}\)
\(\Rightarrow A>\frac{1}{4}\)
đúng thì cho mik nha
2 tháng 4 2022
\(A=\frac{1}{151}+\frac{1}{152}+...+\frac{1}{200}\) ( gồm 50 số hạng )
Ta thấy : \(\frac{1}{151}>\frac{1}{152}>...>\frac{1}{200}\)
\(\Rightarrow\frac{1}{151}+\frac{1}{152}+...+\frac{1}{200}>\frac{1}{200}+\frac{1}{200}+...+\frac{1}{200}\) ( gồm 50 số hạng \(\frac{1}{200}\))
\(\Rightarrow\frac{1}{151}+\frac{1}{152}+...+\frac{1}{200}>\frac{1}{200}.50\)
\(\Rightarrow\frac{1}{151}+\frac{1}{152}+...+\frac{1}{200}>\frac{50}{200}\)
\(\Rightarrow\frac{1}{151}+\frac{1}{152}+...+\frac{1}{200}>\frac{1}{4}\)
Hay \(A>\frac{1}{4}\)
Vậy \(A>\frac{1}{4}\)
_HT_
PT
1
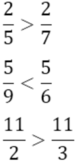
\(3^{152}=3,....^{72}\)
\(4^{112}=2,......^{67}\)
vì \(3^{152}\)có phần nguyên là 3; \(4^{112}\)có phần nguyên là 2
\(\Rightarrow4^{112}< 3^{152}\)
ta có 3^152=9^76>8^76=2^228>2^224=4^112
vậy 3^152>4^112