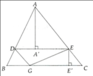
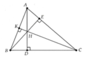
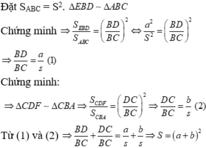Bạn Khoa có một tấm bìa hình tam giác ABC.Hãy giúp bạn Khoa cắt tấm bìa bằng đường thẳng song song với BC cắt các cạnh AB,AC lần lượt tại D,E để diện tích tam giác BDE lớn nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
YN
11 tháng 1 2021
Diện tích hình tam giác ABC là :
\(40.50:2=1000cm^2\)
Nối A với E => Diện tích tam giác AEC là :
\(10.50:2=250cm^2\)
Diện tích tam giác ABE là :
\(1000-250=750cm^2\)
DE dài số xăng-ti-mét là :
\(750.2:40=37,5cm\)
Diện tích tam giác BDE là :
\(37,5.\left(40-10\right):2=562,5cm^2\)
Đáp số : \(562,5cm^2\)
LM
Lê Minh Vũ
CTVHS
11 tháng 1 2021
Diện tích hình ABC là:40 x 50:2=1000(cm2)Nối A với E ta được hình tam giác AEC sẽ có chiều cao là 10 cm mà đáy AC biết rồi .Vậy diện tích hình AEC là:10 x 50:2=250(cm2)Diện tích hình ABE là:1000-250=750(cm2)Đoạn DE dài số cm là:750 x 2:40=37,5(cm)Diện tích hình BDE là:37,5 x (40-10):2=562,5(cm2)Đáp số:562,5 cm2
9 tháng 1 2022
[mình viết tắt]
s aeb là
40x50:2-50x10;2=750[m2]
s bde là;
[750:40]x[40-10];2=281,25[m2]
2 tháng 10 2016
Nối \(AE\), tam giác \(EAC\) có chiều cao bằng độ dài đoạn \(AD=10cm\).
Diện tích tam giác \(EAC\) bằng:
\(\frac{50\times10}{2}=250\left(cm^2\right)\)
Diện tích tam giác \(ABC\) bằng:
\(\frac{50\times40}{2}=1000\left(cm^2\right)\)
Diện tích tam giác \(BAE\) ( bằng diện tích tam giác \(ABC\) trừ đi diện tích tam giác \(EAC\) ):
\(1000-250=750\left(cm^2\right)\)
Chiều cao \(ED\) của tam giác \(BAE\) bằng:
\(\frac{750\times2}{40}=37,5\left(cm\right)\)
Độ dài cạnh \(BC\) bằng:
\(50-10=40\left(cm\right)\)
Vì \(DE\) song song với \(AC\) nên \(DE\) vuông góc với \(BD\). Vậy tam giác \(BDE\) là tam giác vuông tại \(D\) và có diện tích bằng:
\(\frac{40\times37,5}{2}=750\left(cm^2\right)\)
Đáp số: \(750cm^2\)
2 tháng 10 2016
\(S\) \(ABC:\frac{40\times50}{2}=1000\left(cm^2\right)\)
\(S\) \(AEC:\frac{50\times10}{2}=250\left(cm^2\right)\)
\(S\) \(ABE:1000-250=750\left(cm^2\right)\)
\(DE:\frac{750\times2}{40}=37,5\left(cm\right)\)
\(S\) \(BDE:\frac{37,5\times30}{2}=562,5\left(cm^2\right)\)