Giúp mk bài này vs ạ, mk đang cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




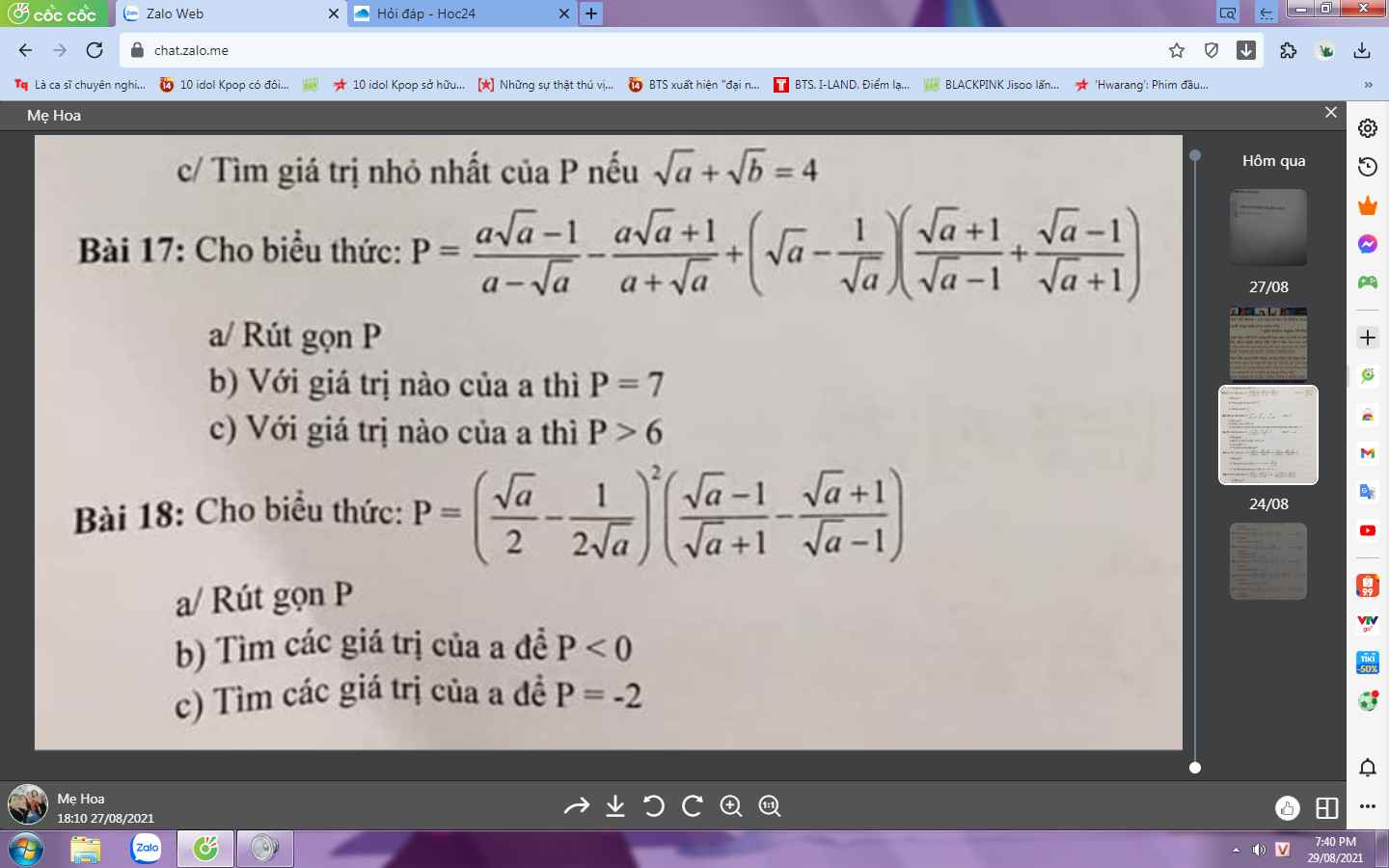
Bài 18:
a: Ta có: \(P=\left(\dfrac{\sqrt{a}}{2}-\dfrac{1}{2\sqrt{a}}\right)^2\cdot\left(\dfrac{\sqrt{a}-1}{\sqrt{a}+1}-\dfrac{\sqrt{a}+1}{\sqrt{a}-1}\right)\)
\(=\dfrac{\left(\sqrt{a}-1\right)^2\cdot\left(\sqrt{a}+1\right)^2}{4a}\cdot\dfrac{a-2\sqrt{a}+1-a-2\sqrt{a}-1}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)
\(=\dfrac{\left(a-1\right)\cdot\left(-4\right)\cdot\sqrt{a}}{4a}\)
\(=\dfrac{-a+1}{\sqrt{a}}\)
b: Để P<0 thì -a+1<0
\(\Leftrightarrow-a< -1\)
hay a>1
c: Để P=-2 thì \(-a+1=-2\sqrt{a}\)
\(\Leftrightarrow-a+1+2\sqrt{a}=0\)
\(\Leftrightarrow a-2\sqrt{a}+1=2\)
\(\Leftrightarrow\left(\sqrt{a}-1\right)^2=2\)
\(\Leftrightarrow\sqrt{a}-1=\sqrt{2}\)
hay \(a=3+2\sqrt{2}\)
Bài 17:
a: Ta có: \(P=\dfrac{a\sqrt{a}-1}{a-\sqrt{a}}-\dfrac{a\sqrt{a}+1}{a+\sqrt{a}}+\left(\sqrt{a}-\dfrac{1}{\sqrt{a}}\right)\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-1}+\dfrac{\sqrt{a}-1}{\sqrt{a}+1}\right)\)
\(=\dfrac{a+\sqrt{a}+1-a+\sqrt{a}-1}{\sqrt{a}}+\dfrac{a-1}{\sqrt{a}}\cdot\dfrac{a+2\sqrt{a}+1+a-2\sqrt{a}+1}{a-1}\)
\(=2+\dfrac{2a+2}{\sqrt{a}}\)
\(=\dfrac{2a+2\sqrt{a}+2}{\sqrt{a}}\)

f: =-1/8-7/6+3/4-1
=-3/24-28/24+18/24-1
=-31/24+18/24-1
=-13/24-1=-37/24
g: \(=6\cdot\dfrac{-8}{27}-3\cdot\dfrac{4}{9}+\dfrac{4}{3}+4\)
=-48/27+4
=108/27-48/27
=60/27
=20/9
h: \(=\left[6\cdot\dfrac{1}{9}+1+1\right]\cdot\left(-3\right)-1\)
=(2/3+2)*(-3)-1
=-2-6-1
=-3-6=-9

\(n_{H_2}=\dfrac{0,224}{22,4}=0,01\left(mol\right)\\
pthh:2R+2H_2O\rightarrow2ROH+H_2\)
0,02 0,01 (mol)
\(\Rightarrow M_R=0,78:0,02=39\left(\dfrac{g}{mol}\right)\)
mà R hóa trị I => R là K

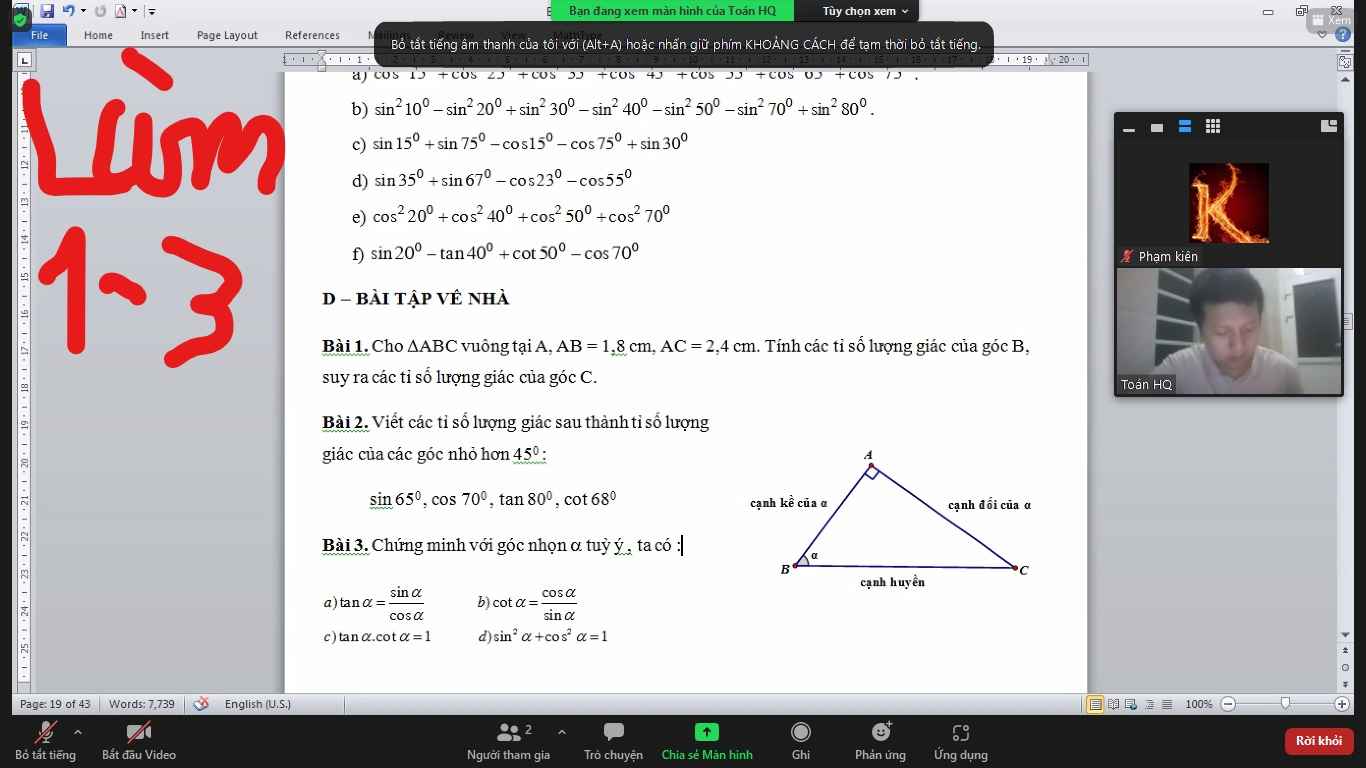
sin 650=cos 350
\(cos70^0=sin30^0\)
\(tan80^0=cot20^0\)
\(cot68^0=tan32^0\)

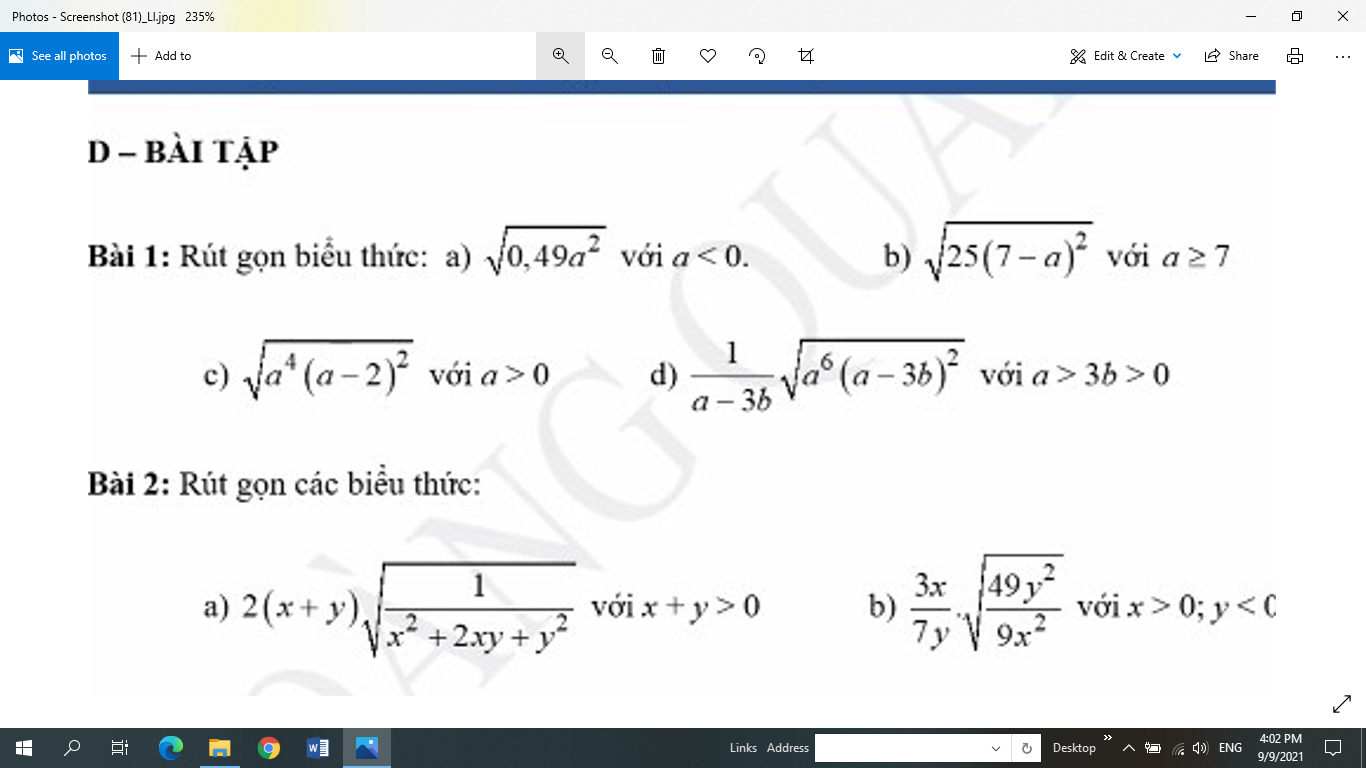
Bài 1:
a: \(\sqrt{0.49a^2}=-0.7a\)
b: \(\sqrt{25\left(a-7\right)^2}=5a-35\)
c: \(\sqrt{a^4\left(a-2\right)^2}=a^2\cdot\left(a-2\right)\)
d: \(\dfrac{1}{a-3b}\cdot\sqrt{a^6\left(a-3b\right)^2}\)
\(=\dfrac{1}{a-3b}\cdot a^3\cdot\left(a-3b\right)=a^3\)
Bài 2:
a: \(2\left(x+y\right)\cdot\sqrt{\dfrac{1}{x^2+2xy+y^2}}\)
\(=2\left(x+y\right)\cdot\dfrac{1}{x+y}\)
=2
b: \(\dfrac{3x}{7y}\cdot\sqrt{\dfrac{49y^2}{9x^2}}\)
\(=\dfrac{3x}{7y}\cdot\dfrac{-7y}{3x}\)
=-1



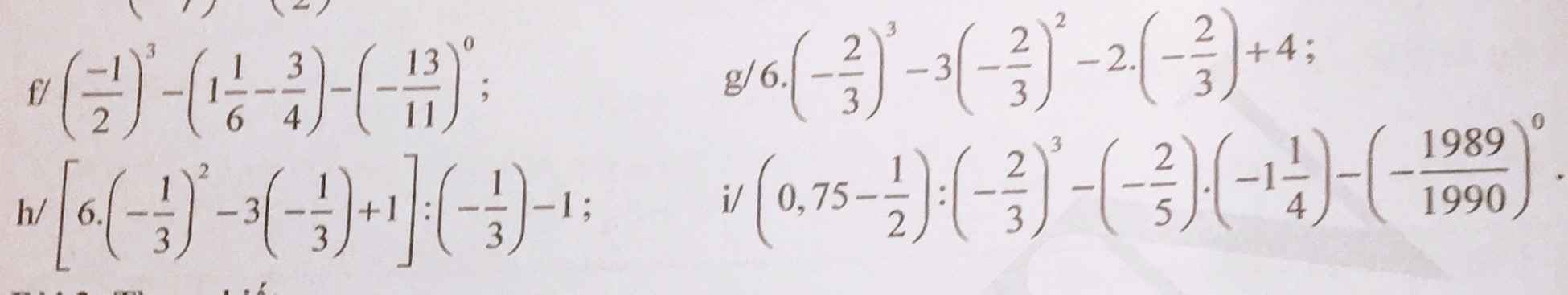

Đề là gì?