giải bất phương trình sau: a, x^2-5x+6<0
b, x/(x-2)+(x+2)/x>2
c, (x-3)/(x+5)+(x+5)/(x-3)<2
mk đang cần gấp mọi người giúp mk nha
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`|5x| = - 3x + 2`
Nếu `5x>=0<=> x>=0` thì phương trình trên trở thành :
`5x =-3x+2`
`<=> 5x +3x=2`
`<=> 8x=2`
`<=> x= 2/8=1/4` ( thỏa mãn )
Nếu `5x<0<=>x<0` thì phương trình trên trở thành :
`-5x = -3x+2`
`<=>-5x+3x=2`
`<=> 2x=2`
`<=>x=1` ( không thỏa mãn )
Vậy pt đã cho có nghiệm `x=1/4`
__
`6x-2<5x+3`
`<=> 6x-5x<3+2`
`<=>x<5`
Vậy bpt đã cho có tập nghiệm `x<5`

hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn


a) \(5x\left(x-3\right)^2-5\left(x-1\right)^3+15\left(x-4\right)\left(x+4\right)\le10\)
\(\Leftrightarrow5x\left(x^2-6x+9\right)-5\left(x^3-3x^2+3x-1\right)+15\left(x^2-16\right)\le10\)
\(\Leftrightarrow5x^3-30x^2+45x-5x^3+15x^2-15x+5+15x^2-240\le10\)
\(\Leftrightarrow\left(5x^3-5x^3\right)-\left(30x^2-15x^2-15x^2\right)-\left(45x-15x\right)+5-240\le10\)
\(\Leftrightarrow30x-235\le10\)
\(\Leftrightarrow30x\le10+235\)
\(\Leftrightarrow30x\le245\)
\(\Leftrightarrow30x:30\le245:30\)
\(\Leftrightarrow x\le\dfrac{49}{6}\)
Vậy nghiệm của bất phương trình là: \(x\le\dfrac{49}{6}\)
b) \(\left(3x-2\right)\left(9x^2+6x+4\right)+27x\left(\dfrac{1}{3}-x\right)\left(\dfrac{1}{2}+x\right)\ge1\)
\(\Leftrightarrow27x^3-8+27x\left(\dfrac{1}{9}-x^2\right)\ge1\)
\(\Leftrightarrow27x^3-8+3x-27x^3\ge1\)
\(\Leftrightarrow\left(27x^3-27x^3\right)-8+3x\ge1\)
\(\Leftrightarrow-8+3x\ge1\)
\(\Leftrightarrow3x\ge1+8\)
\(\Leftrightarrow3x\ge9\)
\(\Leftrightarrow3x:3\ge9:3\)
\(\Leftrightarrow x\ge3\)
Vậy nghiệm của bất phương trình là \(x\ge3\)
a: =>5x(x^2-6x+9)-5(x^3-3x^2+3x-1)+15(x^2-16)<=10
=>5x^3-30x^2+45x-5x^3+15x^2-15x+5+15x^2-240<=10
=>30x-235<=10
=>30x<=245
=>x<=49/6
b: =>27x^3-8+27x(1/9-x^2)>=1
=>27x^3-8+3x-27x^3>=1
=>3x>=9
=>x>=3

a: 3x-5>15-x
=>4x>20
hay x>5
b: \(3\left(x-2\right)\left(x+2\right)< 3x^2+x\)
=>3x2+x>3x2-12
=>x>-12

\(f\left(x\right)=\dfrac{\left(3x-4\right)\left(2x-3\right)}{\left(x^2-5x+6\right)\left(5-x\right)}>0\)
\(\Leftrightarrow\dfrac{\left(3x-4\right)\left(2x-3\right)}{\left(x-2\right)\left(x-3\right)\left(5-x\right)}>0\)
Bảng xét dấu:
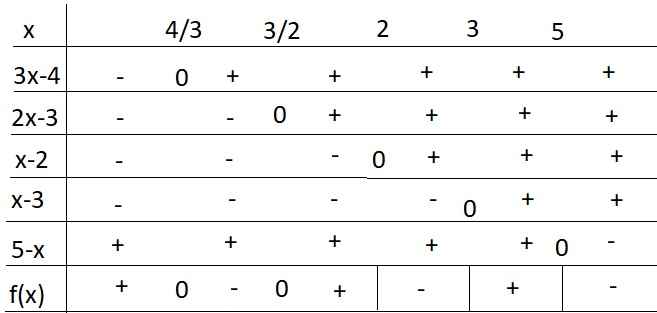
Từ bảng xét dấu ta thấy nghiệm của BPT là: \(\left[{}\begin{matrix}x< 5\\\dfrac{3}{2}< x< 2\\3< x< 5\end{matrix}\right.\)

\(x-\frac{2}{4}-\frac{2}{3}\ge5x-\frac{9}{12}\)
\(\Leftrightarrow x-\frac{7}{6}\ge5x-\frac{3}{4}\)
\(\Leftrightarrow-4x\ge\frac{5}{12}\)
\(\Leftrightarrow-\frac{5}{56}\ge x\)
\(a,x\left(x-5\right)+6< 0\Leftrightarrow\left(x+6\right)\left(x-5\right)< 0\)
\(\orbr{\begin{cases}x+6< 0\\x-5< 0\end{cases}\Leftrightarrow\orbr{\begin{cases}x< -6\\x< 5\end{cases}}}\)
\(b,x^2+\left(x-2\right)\left(x+2\right)>2x\left(x-2\right)\)
\(\Leftrightarrow x^2+x^2-4>2x^2-4x\Leftrightarrow-4>-4x\)
\(\Leftrightarrow-4x< -4\Rightarrow x>1\)
\(c,\left(x-3\right)\left(x-3\right)+\left(x+5\right)\left(x+5\right)< 2\left(x-3\left(x+5\right)\right)\)
\(\Leftrightarrow x^2-6x+9+x^2+10x+25< 2x^2+4x-30\)
\(\Leftrightarrow2x^2-2x^2+4x-4x< -30-34\)
\(\Leftrightarrow0x< -64\)
bất phương trình vô nghiệm