Cho hai khoảng A = (m; m + 1) và B(3; 5). Tìm m để A ∪ B là một khoảng. Hãy xác định khoảng đó.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


- Nếu m = 5 thì A ∩ B = 151;
- Nếu m < 5 thì A ∩ B = Ø;
- Nếu m > 5 thì A ∩ B = [5; m];
Chúc bạn học tốt ~
- Nếu m = 5 thì A ∩ B = 151;
- Nếu m < 5 thì A ∩ B = Ø;
- Nếu m > 5 thì A ∩ B = [5; m];
Chúc bạn học tốt ~

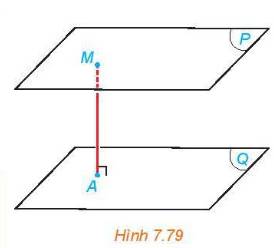
a) Khi một điểm M thay đổi trên đường thẳng m, khoảng cách từ M đến đường thẳng n không thay đổi vì m//n.
b) Vì (P)//(Q) nên các đường thẳng trên mặt (P) đều song song với (Q).
=>Khoảng cách từ M đến (Q) không thay đổi khi M dịch chuyển

a)Khoảng vân: \(i=\dfrac{\lambda D}{a}\)
\(\Rightarrow0,8\cdot10^{-3}=\dfrac{\lambda\cdot2}{1\cdot10^{-3}}\Rightarrow\lambda=4\cdot10^{-7}m=0,4\mu m\)
b)Tần số ánh sáng đơn sắc dùng trong thí nghiệm:
\(f=\dfrac{v}{\lambda}=\dfrac{c}{\lambda}=\dfrac{3\cdot10^8}{4\cdot10^{-7}}=7,5\cdot10^{14}Hz\)


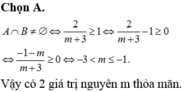
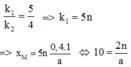
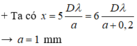
A ∪ B là một khoảng khi và chỉ khi A ∩ B ≠ Ø.
Ta thấy A ∩ B = Ø Khi m + 1 ≤ 3 hoặc m ≥ 5 tức là khi m ≤ 2 hoặc m ≥ 5.
Vậy nếu 2 < m < 5 thì A ∪ B là một khoảng.
Cụ thể hơn ta tìm được:
- Nếu 2 < m ≤ 3 thì A ∪ B là khoảng (m; 5);
- Nếu 3 < m ≤ 4 thì A ∪ B là khoảng (3; 5);
- Nếu 4 < m < 5 thì A ∪ B là khoảng (3; m + 1).
A ∪ B là một khoảng khi và chỉ khi A ∩ B ≠ Ø. Ta thấy A ∩ B = Ø Khi m + 1 ≤ 3 hoặc m ≥ 5 tức là khi m ≤ 2 hoặc m ≥ 5. Vậy nếu 2 < m < 5 thì A ∪ B là một khoảng. Cụ thể hơn ta tìm được: - Nếu 2 < m ≤ 3 thì A ∪ B là khoảng (m; 5); - Nếu 3 < m ≤ 4 thì A ∪ B là khoảng (3; 5); - Nếu 4 < m < 5 thì A ∪ B là khoảng (3; m + 1).